Prüfung von Messwerten – Biotechberatung

Einführende Bemerkungen

Im Kapitel über Mittelwerte und die Standardabweichung haben wir das arithmetische Mittel sowie die Standardabweichung als wichtige Maßzahlen zur biometrischen Beschreibung einer Menge von Messwerten kennengelernt. In den Kapiteln über Wahrscheinlichkeiten und Häufigkeiten hatte ich versucht zu erläutern, wie man auf Grund der Regeln für das Rechnen mit Wahrscheinlichkeiten zur Überschreitungswahrscheinlichkeit und damit zum biometrischen Test kommt und dann mittels solcher Tests z. B. prüfen kann, ob sich die an zwei verschiedenen Stichproben ausgezählten Häufigkeiten signifikant unterscheiden.

Probleme, deren Lösung nur durch einen biometrischen Test möglich ist, ergeben sich auch dann immer wieder, wenn nicht Häufigkeiten ausgezählt, sondern an den einzelnen Versuchsobjekten Messungen durchgeführt werden. Besonders wichtig ist auch hier der Fall, dass Messungen an zwei Stichproben durchgeführt werden, die sich in einem Merkmal y eindeutig unterscheiden, beispielsweise weil es gesunde und kranke oder behandelte und unbehandelte Tiere sind. Die Messungen betreffen dann andere Merkmale wie Körpergewicht, Körpertemperatur, oder die Konzentration bestimmter Stoffe im Blut, in einzelnen Organen oder in der Milch, demnach quantitativ variierende Merkmale. Es ist dann vielfach wichtig zu wissen, ob sich der Unterschied im Merkmal y auf eines dieser Sekundärmerkmale auswirkt, ob demnach zwischen den Mitteln der beiden Stichproben und eine echte Differenz besteht bzw. ob die gefundene Differenz signifikant ist.

Natürlich gibt es außer dem hier skizzierten Problem noch viele andere Fragestellungen, zu deren Lösung man einen biometrischen Test benötigt. Der Vergleich der Mittel zweier Messwertreihen kann jedoch als ein Basisproblem angesehen werden, weil seine Lösung einen Ansatzpunkt für die Erörterung ähnlicher Aufgaben bildet.

Den Hintergrund der Betrachtungen sollen zwei Reihen von Messwerten geben, bei denen es sich um die Geburtsgewichte von Kälbern verschiedener Rassen handeln könnte. Die Einzelwerte, ihre Mittel, Varianzen und Standardabweichungen zeigt die folgende Tabelle.

Stichprobe A	Stichprobe B
47	34
31	41
42	34
44	26
39	31

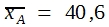
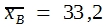
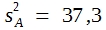
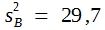
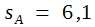
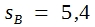
Vor einer Situation, wie sie die Tabelle zeigt, steht man in den biologischen Wissenschaften oft. Immer wieder ist die Variation innerhalb der Stichproben so groß, dass sich die Einzelwerte verschiedener Stichproben überlappen. Bei dem gezeigten Beispiel reichen die Messungen in Stichprobe A von 31 bis 47, die von Stichprobe B von 26 bis 41. Dennoch gibt es eine deutliche Differenz zwischen den beiden Mittelwerten. 40,6 – 33,2 = 7,4. Ist nun diese Differenz signifikant? Darf man annehmen, dass sie echt ist? Würde man bei einer Wiederholung der Messungen mit hoher Wahrscheinlichkeit zu einem gleich gerichteten Unterschied zwischen beiden Rassen kommen?

In der Physik ist es in ähnlichen Situationen oft möglich, das Messverfahren zu verbessern und dadurch die Variation innerhalb der Messreihen so zu vermindern, dass die Ergebnisse eindeutig werden. In der Biologie bildet jedoch die natürliche Variation der Organismen zumeist die Hauptursache für das Überschneiden der Verteilungsbereiche. Hier nützt es kaum, genauer zu wiegen. Man kann nur versuchen, mithilfe eines biometrischen Tests zu einer Wahrscheinlichkeitsaussage zu kommen.

Fehlerfortpflanzungsgesetze

Auch bei Messwertstichproben bildet die Standardabweichung die Grundlage für biometrische Tests. Dazu sei zunächst kategorisch formuliert. Unter der Voraussetzung, dass die Einzelwerte normal verteilt sind, bestehen zwischen den Überschreitungswahrscheinlichkeiten und bestimmten, in σ angegebenen Abweichungen gleiche Beziehungen wie in der Binomialverteilung.

Wenn bei einer Binomialverteilung der Stichprobenumfang immer größer wird, müssen die einzelnen Wahrscheinlichkeitswerte zwangsläufig immer kleiner werden. Die gilt auch bei Ereignissen in der Nähe des Erwartungswertes. Es wird dann sinnlos, mit dem Begriff der Ereigniswahrscheinlichkeit zu operieren, weil zu viele Einzelwerte, die alle nahe bei Null liegen, addiert werden müssten, um zu Überschreitungswahrscheinlichkeiten zu kommen. Man ersetzt ihn durch den Begriff der Wahrscheinlichkeitsdichte und errechnet den Flächeninhalt von Abschnitten unter der Verteilungskurve.

Man kann die Wahrscheinlichkeitsdichte nach der folgenden Formel für jeden einzelnen Punkt berechnen:

(24)

Diese Formel liefert uns Relativwerte, die Höhe der Verteilungskurve an bestimmten Punkten (=y_x) relativ zur Gipfelhöhe bei y₀, dem Erwartungswert oder Mittel.

Um zu numerischen Werten zu kommen, muss man für y₀ und σ bestimmte Zahlen einsetzen. Am nahe liegendsten ist es, y₀ und σ = 1 zu setzen. Die Formel (24) vereinfacht sich dann wie folgt:

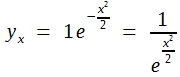
Für x = 1 ergibt sich:

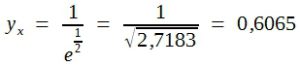
Das bedeutet, dass die Höhe der Verteilungskurve im Abstand von 1 σ vom Mittel 60,65% der Gipfelhöhe ist, und zwar sowohl links als auch rechts von µ. Ebenso errechnet man für:

x = 2 : y_x = 13,53%

x = 3 : y_x = 1,11%

Wenn man in dieser Weise genügend viele Punkte errechnet hat, kann man die Kurve zeichnen und sieht dann, dass sie eine charakteristische Form hat, wie eine Glocke. Sie wird deshalb gern als Glockenkurve bezeichnet, sie kennzeichnet die Normalverteilung.

Wichtiger als die Errechnung von Relativwerten für die Höhe bestimmter Punkte der Normalverteilung ist es, den Inhalt bestimmter Flächenabschnitte zu kennen. Wählt man Abschnitte, die vom Gipfel nach beiden Seiten gleich weit reichen, so erhält man Relativwerte für Nichtüberschreitungswahrscheinlichkeiten. Es ist üblich, y₀ nicht gleich 1 zu setzen sondern:

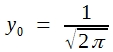
Durch diesen Trick erreicht man nämlich, dass die Gesamtfläche unter der Kurve1 beträgt. Aus Formel (24) wird dann:

(25)

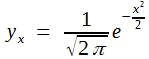
Für x = 0 , also für den Gipfelpunkt, findet man dann die Höhe 0,3989.

Die direkte Berechnung des Inhalts bestimmter Abschnitte unter dieser Kurve durch Integration bereitet einige Schwierigkeiten. Stets ist es aber möglich, genügend viele Ordinaten zu berechnen, die Kurve in schmale Säule zu zerlegen und die Säuleninhalte zu addieren. Berechnet man dies für Flächen, die von der Mitte, d.h. vom arithmetischen Mittel aus gleich weit nach beiden Seiten reichen, und subtrahiert die Ergebnisse von 1, so erhält man Überschreitungswahrscheinlichkeiten. Bitte rechnen Sie solche P-Werte aus, Sie werden finden, dass Ihre Ergebnisse den in der Tabelle „Überschreitungswahrscheinlichkeiten für Abweichungen bestimmter Größe in t“ nahezu übereinstimmen.

Aus vorgenannter Tabelle kann zunächst übernommen werden, wie wahrscheinlich es ist, dass ein weiterer Wert aus einer Grundgesamtheit mit bekanntem µ und σ innerhalb oder außerhalb eines bestimmten Intervalls liegt. Beispielsweise erwartet man ihn mit 4,5%-iger Wahrscheinlichkeit außerhalb und demnach mit 95,5%-iger Wahrscheinlichkeit innerhalb von und .

Von M. W. Toews – Eigenes Werk, based (in concept) on figure by Jeremy Kemp, on 2005-02-09, CC BY 2.5, Link

Derartige Angaben benötigt man z. B., um biometrisch korrekt festzustellen, ob bestimmte Körperfunktionen eines Tieres, wie Temperatur, Puls, Atemtätigkeit normal sind. Man kennt hier das arithmetische Mittel und die Standardabweichung aus umfangreichen Untersuchungen ziemlich genau. Demzufolge kann man für solche Merkmale den Mutungsbereich errechnen. Das ist der Bereich, in dem 95% oder 99% aller normalen Werte zu erwarten sind, sodass ein außerhalb liegender Einzelwert als signifikant abweichend bezeichnet werden darf bzw. als „nicht mehr normal“.

Das einleitend zu diesem Kapitel aufgeworfene Problem war aber auch nicht, abzuschätzen, in welchem Bereich weitere Einzelwerte einer bestimmten Messung erwartet werden dürfen, sondern ob sich die Mittelwerte zweier Stichproben signifikant unterscheiden. – Um diese Frage beantworten zu können, ist zu klären, wie sich die Variabilität der Einzelwerte auf die Varianz von Summen, Mitteln und Differenzen auswirkt. Man bezeichnet dies als Fehlerfortpflanzung.

Zur Erläuterung der Fehlerfortpflanzungsgesetze bedient man sich zweckmäßigerweise eines Zufallsexperimentes, z. B. des besprochenen Experiments mit einem regulären Würfel. Mittel und Varianz der resultierenden Wahrscheinlichkeitsverteilung zeigt die folgende Tabelle:

Tabelle 12: Mittel und Varianz der Wahrscheinlichkeitsverteilung beim Würfelwurf

Augenzahl(x_i)	p_i	x_ip_i	(x_i-E)	(x_i-E)²p_i
1	1/6	1/6	-5/2	25/24
2	1/6	2/6	-3/2	9/24
3	1/6	3/6	-1/2	1/24
4	1/6	4/6	1/2	1/24
5	1/6	5/6	3/2	9/24
6	1/6	6/6	5/2	25/24

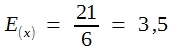
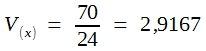
Von diesem Ergebnis ausgehend soll nun ausgerechnet werden, wie groß die Varianz der Augensummen ist, die sich beim Würfeln mit 2 Würfeln ergeben. Die Wahrscheinlichkeiten für die daraus resultierenden 11 Ereigniskombinationen wurden bereits demonstriert. Die Ergebnisse finden Sie in Tabelle 13

Tabelle 13: „Mittel und Varianz der Wahrscheinlichkeitsverteilung aus den Augensummen beim Werfen mit 2 Würfeln“

Augensummen (x_i)	p_i	x_ip_i	(x_i-E)	(x_i-E)²p_i
2	1/36	2/36	-5	25/36
3	2/36	6/36	-4	32/36
4	3/36	12/36	-3	27/36
5	4/36	20/36	-2	16/36
6	5/36	30/36	-1	5/36
7	6/36	42/36	0	–
8	5/36	40/36	1	5/36
9	4/36	36/36	2	16/36
10	3/36	30/36	3	27/36
11	2/36	22/36	4	32/36
12	1/36	12/36	5	25/36

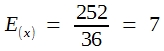
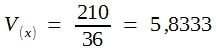
Wie ersichtlich, ist die Varianz der Augensummen zweier Würfel genau doppelt so groß wie die Varianz der Ereignisse beim 1-Würfel-Modell. Bitte beachten Sie, dass es sich hier nicht um ein empirisch ermitteltes und daher mit Zufälligkeiten behaftetes Ergebnis handelt, sondern um echte Wahrscheinlichkeitswerte aus einem nur gedanklich durchführbaren Zufallsexperiment. Es darf daher behauptet werden (wenngleich es sich natürlich nicht um einen vollwertigen mathematischen Beweis handelt), dass die Varianz einer Summe der Varianzen der einzelnen Summanden entspricht:

Daraus aber folgt, dass die Standardabweichung einer Summe mit der sogenannten pythagoreischen Summe ihrer Einzelvarianzen übereinstimmt:

(26)

Um zu einer ähnlichen Formel für die Varianz und Standardabweichung des arithmetischen Mittels zu kommen, braucht man nur zu bedenken, dass die Augensummen in Tabelle 13 durch 2 zu dividieren sind. Demnach werden die mittleren Augenzahlen halb so groß und die Abweichungsquadrate betragen nur ein Viertel. Man erhält in logischer Erweiterung dieser Überlegungen:

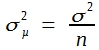
und für die Standardabweichung:

(27)

Um zu ähnlichen Formeln für die Standardabweichung von Differenzen zu kommen, müsste man zunächst die Wahrscheinlichkeiten für das Auftreten verschieden großer Differenzen beim 2-Würfel-Modell zusammenstellen. Es zeigt sich, dass auch hier extrem große Differenzen seltener zu finden sind als weniger große, denn man erhält:

eine Differenz 5 nur bei den Kombinationen 1 : 6 und 6 : 1

eine Differenz 4 bei den Kombinationen 1 : 5, 2 : 6, 5 : 1 und 6 : 2.

Führt man diese Überlegungen fort, so zeigt sich, dass die Wahrscheinlichkeiten für Differenzen bestimmter Größe genauso sind wie die für gleich große Abweichungen vom arithmetischen Mittel. Demnach ist die Varianz der Differenz beim 2-Würfel-Modell ebenso groß wie die Varianz der Summe:

und daher:

(28)

In der Praxis geht es zumeist nicht um die Verteilung der Differenzen zufällig ausgewählter Einzelwerte aus einer Grundgesamtheit, sondern um die Differenz zwischen Stichprobenmitteln. In Kombination der Formeln (27) und (28) erhält man:

(29)

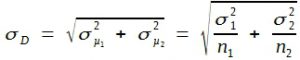
Die Ausrechnung des Flächeninhaltes unter bestimmten Abschnitten der Normalverteilungskurve erlaubt demnach nicht nur die Bildung von Mutungsbereichen bzw. die Berechnung von Überschreitungswahrscheinlichkeiten für Einzelwerte, sondern auch für Stichprobenmittel und deren Differenzen. – Wenn es eine Grundgesamtheit mit µ = 40 und σ = 5 gibt, so liegen nach Tabelle 9 z. B. 31,7% aller Einzelmesswerte außerhalb und folglich 68,3% der Werte innerhalb eines Intervalls von

Stellen wir aus dieser Grundgesamtheit Stichproben von je 4 Einzelwerten zusammen, so ist die Standardabweichung dieser Mittel nach Formel (27):

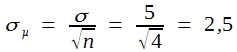
Das bedeutet aber, dass das gleiche Intervall dann dem Doppelten der Standardabweichung der Mittel entspricht, sodass nur 4,5% dieser Mittel außerhalb liegen sollten.

Der Erwartungswert für Differenzen zwischen solchen zufällig zusammengestellten Stichproben ist natürlich = 0. Fragen wir, wie wahrscheinlich es ist, dass die Differenz größer als 5 wird, so ergibt sich die Antwort aus Formel (29). Die Standardabweichung unserer Differenz beträgt demnach:

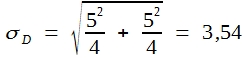
Eine Differenz von 5 entspricht demnach dem 1,41-fachen der Standardabweichung. Außerhalb dieser Grenzen liegen nach Tabelle 9 aber 15,7% aller Werte.

Bitte beachten Sie, dass die Varianz der Stichprobenmittel die Ursache für die Verminderung der Abweichungsquadratsumme beim Quadrieren der Differenzen von diesen Mitteln aus ist. Die Gesamtsumme der Abweichungsquadrate besteht daher aus den folgenden beiden Komponenten:

Die rechte Komponente ist im Durchschnitt 1/n der Gesamtsumme. Die in Abschnitt „Variationsmaße“ erläuterte Formel findet hier ihre mathematische Grundlage.

Prüfung der Differenz zwischen Stichprobenmitteln

Das Ziel der Erörterungen des vorhergehenden Abschnittes sollte die Entwicklung eines Verfahrens zur biometrischen Überprüfung der Differenz zweier Stichprobenmittel sein, z.B. der in Tabelle 11 angegebenen Mittel. Im Prinzip wäre dazu Formel (29) geeignet. Man kann nämlich annehmen, dass die natürliche Variabilität der Organismen sich aus einer sehr großen Zahl sogenannter „Elementarfehler“ ergibt. Wenn weiter angenommen wird, dass diese unmessbar kleinen Elementarfehler voneinander unabhängig sind und sich nach den Gesetzen des Zufalls entweder positiv oder negativ auswirken, entsteht eine Binomialverteilung mit sehr großem n, eben eine Normalverteilung der gemessenen Einzelwerte um den Mittelwert der Grundgesamtheit.

Ist Ihnen aufgefallen, dass im vorhergehenden Abschnitt bei den Formeln (26) bis (29) µ und σ als Symbole verwendet wurden, während in Tabelle 11 und s steht? Dieser Unterschied in der Bezeichnungsweise ist nicht zufällig. In der Tat sind die in Tabelle 11 angegebenen Mittel und Standardabweichungen nicht die Parameter einer Grundgesamtheit, sondern nur Schätzwerte dafür. Diese Schätzwerte sind zwar unverzerrt, können aber bei so kleinen Stichproben nur geringe Präzision haben. Daraus ergibt sich, dass man nach Formel (29) exakte Überschreitungswahrscheinlichkeiten nur dann errechnen kann, wenn beide σ-Werte bekannt sind. Genügend gute Näherungswerte findet man allerdings auch schon, wenn aus großen Stichproben präzise Schätzwerte errechnet werden konnten. Bei großen Stichproben führt die Formel demnach zu einem approximativen Test, der aber gut genug ist. Es ist allerdings üblich, andere Symbole zu verwenden und die Standardabweichung der Differenz zweier Mittelwerte wie folgt zu formulieren:

(30)

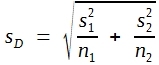
Formel (30) ist allerdings nur dann korrekt, wenn die Unterschiede zwischen den Standardabweichungen zufällig sind.

Man berechnet dann, ebenso wie in Abschnitt 4.7 erläutert, einen t-Wert, indem man die Differenz der beiden Stichprobenmittel durch s_D dividiert:

(31)

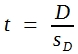
Dieser t-Wert korrespondiert bei großen Stichproben näherungsweise mit den in Tabelle 9 angegebenen Überschreitungswahrscheinlichkeiten.

Es sei angenommen, dass bei je einer größeren Stichprobe zweier Pferderassen die Widerristhöhe mit folgendem Ergebnis gemessen wurde:

Rasse A:

s_A = 8,93

n_A = 240

Rasse B:

s_B = 7,47

n_B = 260

Um zu prüfen, ob sich die beiden Rassen in ihren Widerristhöhen signifikant unterscheiden, rechnet man wie folgt:

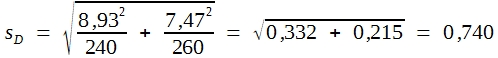
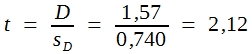
Da der gefundene t-Wert größer als 1,96 ist, darf man behaupten, dass die gefundene Differenz nicht zufällig aufgetreten ist. Somit darf man annehmen, dass die Pferde der Rasse A im Mittel größer sind als die der Rasse B.

Was ändert sich, wenn wir die gleiche Prüfung an kleinen Stichproben durchführen wollen? Es gibt dann keine präzisen Schätzwerte für σ. Es könnte sein, dass in der Stichprobe rein zufällig nur Messwerte auftreten, die in der Nähe des Mittels liegen. Bei einer Vergrößerung der Stichprobe würden vermutlich viele extreme Messwerte dazukommen. Die aus den zuerst gemessenen Werten errechnete Standardabweichung wäre folglich zu klein. Das bedeutet aber, dass auch s_D zu klein, der t-Wert daher zu groß werden muss. Zu oft würde man eine gefundene Differenz als signifikant deklarieren.

Berücksichtigt man die Fehler, die sich bei der Berechnung der Standardabweichung in Stichproben ergeben, so kommt man zu einer Schar von Verteilungskurven, die alle im Zentrum niedriger, an den beiden Schwänzen aber höher sind als die Normalverteilungskurve. Man bezeichnet sie als Studentverteilung. t-Werte, die mit bestimmten Überschreitungswahrscheinlichkeiten korrespondieren, müssen folglich größer als die Normalverteilung sein. Die Unterschiede werden umso deutlicher, je geringer die Präzision des errechneten Schätzwertes für die Standardabweichung der Differenz, des s_D-Wertes ist.

Es ist üblich, auch hier das Konzept der Freiheitsgrade zu verwenden. Der FG der Standardabweichung der Differenz entsprechen der Summe der FG beider s-Werte, also (n₁ – 1) + (n₂ – 1). Die Tabelle 14 zeigt Grenzwerte für 5%, 1% und 0,1% Irrtumswahrscheinlichkeit. Wie ersichtlich, geht die Studentverteilung bei vielen Freiheitsgraden in die in Tabelle 9 dargestellte Normalverteilung über. Daraus folgt, dass die biometrische Prüfung der Differenz der beiden in Tabelle 11 angegebenen kleinen Stichproben formal ebenso durchgeführt werden kann wie bei der größeren, also wie folgt:

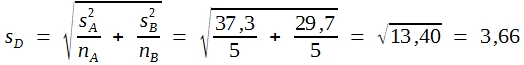
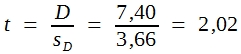
Die Beurteilung des errechneten t-Wertes darf dann aber nicht anhand der P-Werte in Tabelle 9 vorgenommen werden, sondern muss aufgrund der in Tabelle 14 für die betreffende Zahl an Freiheitsgraden angegebenen Grenzwerte erfolgen. Hier haben wir:

Bei 8 Freiheitsgraden entspricht erst ein t-Wert von 2,21 der Signifikanzgrenze von 5%. Somit ist die hier errechnete Differenz von 7,40 noch nicht signifikant. Unter den gegebenen Bedingungen müsste sie dafür größter sein als .

Tabelle 14: t-Verteilung

FG	Überschreitungswahrscheinlichkeit
FG	0,100	0,050	0,010	0,001
1	6,31	12,71	63,66
2	2,92	4,30	9,93	31,60
3	2,35	3,18	5,84	12,94
4	2,13	2,78	4,60	8,61
5	2,02	2,75	4,03	6,86
6	1,94	2,45	3,71	5,96
7	1,90	2,37	3,50	5,41
8	1,86	2,31	3,36	5,04
9	1,83	2,26	3,25	4,79
10	1,81	2,23	3,17	4,59
11	1,80	2,20	3,11	4,44
12	1,78	2,18	3,06	4,32
13	1,77	2,16	3,01	4,22
14	1,76	2,15	2,98	4,14
15	1,75	2,13	2,95	4,07
16	1,75	2,12	2,92	4,02
17	1,74	2,11	2,90	3,97
18	1,73	2,10	2,88	3,92
19	1,73	2,09	2,86	3,88
20	1,73	2,09	2,85	3,85
22	1,71	2,07	2,81	3,79
24	1,71	2,06	2,80	3,75
26	1,71	2,06	2,78	3,71
28	1,70	2,05	2,76	3,67
30	1,70	2,04	2,75	3,65
35	1,69	2,03	2,72	3,59
40	1,68	2,02	2,70	3,55
45	1,68	2,01	2,69	3,52
50	1,68	2,01	2,68	3,50
60	1,67	2,00	2,66	3,46
80	1,67	1,99	2,64	3,42
100	1,66	1,98	2,63	3,39
	1,6448	1,9600	2,5758	3,2905

Einfache Varianzanalyse

Wie bei der biometrischen Prüfung von Häufigkeiten kann man auch hier behaupten, dass der im vorhergehenden Abschnitt erläuterte t-Test veraltet ist. Ein modernes und heute sehr gebräuchliches Testverfahren ist die Varianzanalyse. Wie beim χ²-Test zur Prüfung von Häufigkeiten besteht der Hauptvorteil der VA darin, dass sie überaus erweiterungsfähig ist. Eine erste Erweiterung besteht in der gleichzeitigen Prüfung der Mittel von mehr als zwei Stichproben. – Die Anwendungsmöglichkeiten der Varianzanalyse können aber an dieser Stelle bei weitem nicht vollständig beschrieben werden. Zwei weitere Ansatzpunkte zur Erweiterung des Konzeptes, der Blockversuch und eine einfache faktorielle Anlage, sollen aber wegen ihrer grundsätzlichen Bedeutung in den beiden nächsten Abschnitten noch behandelt werden.

Eigentlich kann man die Varianzanalyse auch als Schnellrechenverfahren bezeichnen. Die Vereinfachungen werden allerdings erst dann wirksam, wenn es sich um die Auswertung von Versuchen von weniger elementarer Struktur handelt, wie sie in der Praxis zwar weit verbreitet vorkommen, aus didaktischen Gründen hier aber nicht besprochen werden können.

Scheinbar unterscheidet sich die Art und Weise der Verarbeitung des Datenmaterials nach der VA so sehr von der Berechnung des t-Wertes, dass vielfach angenommen wird, es handele sich um ein ganz anderes Verfahren, das auch zu anderen Ergebnissen führt. In Wirklichkeit geht es bei beiden Verfahren um die Berechnung der Überschreitungswahrscheinlichkeiten für Differenzen zwischen Stichprobenmitteln. Um die Übereinstimmungen zu demonstrieren, wird das Rechenverfahren zunächst an dem gleichen Beispiel erläutert, das auch für die Beschreibung des t-Testes verwendet wurde.

Schema zur Durchführung einer einfachen Varianzanalyse (Daten aus Tabelle 11)

Man schreibt alle Messwerte geordnet nieder und bildet alle sinnvollen Randsummen. (hier gibt es nur die Prüfgliedsummen und die Totalsumme)

	47	34
	31	41
	42	34
	44	26
	39	31
Summen =	203	166	369

Man berechnet das Subtraktionsglied (= Sutra), das ist das durch N dividierte Quadrat der Totalsumme:

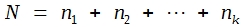
hier N = 5 + 5 = 10

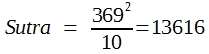
Man errechnet SQ-Total, die Abweichungsquadratsumme der Einzelwerte:

Man errechnet SQ-Prüfglieder, wobei jede Prüfgliedsumme durch das dazugehörige n dividiert werden muss:

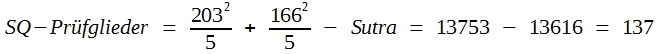
Man errechnet SQ-Fehler durch Subtraktion:

Man trägt die SQ-Werte in eine Varianztabelle ein und errechnet die MQ-Werte, indem man jeden SQ-Wert durch die dazugehörigen FG dividiert. Dabei ist:

FG-Total = N-1

FG-Prüfglieder = k-1

FG-Fehler ergibt sich durch Subtraktion, hier FG-Total – FG-Prüfglieder:

Varianztabelle

	SQ	FG	MQ
Total	405	9
Prüfglieder	137	1	137,0	4,09
Fehler	268	8	33,5

Man errechnet die Prüfgröße „F“, indem man MQ-Prüfglieder durch MQ-Fehler dividiert.

Wie das Schema zeigt, wird zunächst ein universell für alle Komponenten gültiges Subtraktionsglied errechnet, gewissermaßen in Erweiterung des durch Formel (10) beschriebenen Patentverfahrens zur Berechnung der Standardabweichung. Weiterhin werden SQ-Werte, d.h. Abweichungsquadratsummen errechnet, zunächst ein SQ-Total, in die sowohl die Variabilität innerhalb als auch zwischen den Stichproben eingeht. Die Variabilität zwischen den Stichproben ist bei Versuchen mit nur zwei Prüfgliedern zugleich eine Maßzahl für die Differenz der beiden Stichprobenmittel.

Bei einfachen Versuchen gibt es nur 2 Komponenten, nämlich die Variabilität innerhalb und zwischen den Stichproben. Beide Komponenten addieren sich zur SQ-Total, also:

SQ-Total = Komp.A + Komp.B

Demzufolge kann man sich die Rechenarbeit leichter machen, indem man – wie das obige Schema unter Punkt 3 bis 5 zeigt – lediglich SQ-Total und SQ-Prüfglieder errechnet und die andere Komponente dann durch Subtraktion ermittelt:

Komp.B = SQ-Total – Komp.A

Die SQ-Werte sind Abweichungsquadratsummen. Man benötigt dazu die Freiheitsgrade, die sich stets nach dem Konzept der „frei variablen Größen“ bestimmten lassen. Auch die Freiheitsgrade sind additiv, sodass man FG-Fehler ebenso wie SQ-Fehler durch Subtraktion errechnen kann.

Wenn man die SQ-Werte durch die Freiheitsgrade dividiert, erhält man MQ-Werte, und das sind Varianzen. Da MQ-Total in der Regel uninteressant ist, braucht man bei der einfachen Varianzanalyse lediglich MQ-Prüfglieder und MQ-Fehler zu errechnen. MQ-Fehler ist identisch mit dem arithmetischen Mittel der Varianzen der beiden Prüfglieder. Bitte vergleichen Sie mit Tabelle 11. Dort war:

also

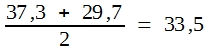
und das ist auch MQ-Fehler in der Varianztabelle des obigen Schemas. Man kann demzufolge MQ-Fehler für die Errechnung der Standardabweichung der Differenz verwenden, wenn man in Formel (30)

setzt.

Bei der VA ist es jedoch üblich, den Test anders durchzuführen. Man hat ja MQ-Prüfglieder, eine Maßzahl für die Variabilität zwischen den Prüfgliedern, für das Ausmaß der Differenzen zwischen den Einzelmitteln zur Verfügung. Deshalb errechnet man den F-Wert:

(32)

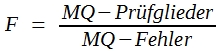
Bei Versuchen mit nur 2 Prüfgliedern ist der F-Wert identisch mit t². Bitte vergleichen Sie mit dem Ergebnis des t-Testes. Dort war t = 2,02 errechnet worden. 2,02² ist aber 4,09, und das ist der F-Wert in der Varianztabelle des obigen Schemas. Somit zeigt sich, dass F-Test und t-Test auf der gleichen Grundkonzeption beruhen. Für die einfache VA lautet diese:

Die Differenzen zwischen den Prüfgliedern erzeugen eine Varianz. Je größer diese Varianz relativ zur mittleren Varianz ist, umso wahrscheinlicher ist es, dass alle Prüfglieder der gleichen Grundgesamtheit entstammen.

Allerdings benötigt man zur Angabe der Überschreitungswahrscheinlichkeiten eine andere Tabelle, eben die F-Tabelle.

Tabelle 15: P = 5 % Grenzwerte der F-Verteilung

FG des Nenners	FG des Zählers
	1		2		3		4		6		8		10
1	161	200		216		225		234		239		242
2	18,51	19,00		19,16		19,25		19,33		19,37		19,39
3	10,13	9,55		9,28		9,12		8,94		8,84		8,78
4	7,71	6,94		6,59		6,39		6,16		6,04		5,96
5	6,61	5,79		5,41		5,19		4,95		4,82		4,74
6	5,99	5,14		4,76		4,53		4,28		4,15		,06
7	5,59	4,74		4,35		4,12		3,87		3,73		3,63
8	5,32	4,46		4,07		3,84		3,58		3,44		3,34
9	5,12	4,26		3,86		3,63		3,37		3,23		3,13
10	4,96	4,10		3,71		3,48		3,22		3,07		2,97
12	4,75	3,88		3,49		3,26		3,00		2,85		2,76
14	4,60	3,74		3,34		3,11		2,85		2,70		2,60
16	4,49	3,63		3,24		3,01		2,74		2,59		2,49
18	4,41	3,55		3,16		2,93		2,66		2,51		2,41
20	4,35	3,49		3,10		2,87		2,60		2,45		2,35

Bei der F-Tabelle muss man beachten, dass es sowohl auf die Freiheitsgrade des Zählers (in der Regel = Zahl der Prüfglieder – 1) als auch auf die des Nenners in Formel (32) ankommt. Für Versuche mit nur 2 Prüfgliedern gilt dort die 1. Spalte der Tabelle, und hier sind die Werte mit den Quadraten der Zahlen in Tabelle 14 für P = 5 % identisch. Für 8 FG findet man dort einen t-Wert von 2,31. In der F-Tabelle steht an analoger Position 5,32. Demnach ist der für das Beispiel „Schema zur einfachen Durchführung einer einfachen Varianzanalyse“ F-Wert von 4,09 nicht signifikant.

Blockversuch

Bereits mehrfach war betont worden, dass der Hauptvorteil der Varianzanalyse in ihrer Erweiterungsfähigkeit besteht. In diesem Abschnitt sollen zwei Erweiterungen des Konzeptes besprochen werden. Zunächst geht es um die gleichzeitige Prüfung von mehr als 2 Prüfgliedern. Dazu sind in Tabelle 16 die Daten eines Versuchs mit 4 Prüfgliedern und je 3 Wiederholungen zusammengestellt worden. Es könnte sich hier z.B. um die mittlere tägliche Gewichtszunahme in einem Fütterungsversuch handeln, bei dem je 3 Ferkel in 4 Gruppen gefüttert wurden.

Tabelle 16: Daten eines Versuches mit 4 Prüfgliedern und je 3 Wiederholungen

Prüfglied	A	B	C	D
	31	25	24	20	100
	37	27	28	24	116
	46	29	41	28	144
Summen	114	81	93	72	360

In der Tabelle wurden bereits die Prüfgliedsummen und die Gesamtssumme gebildet. Analog zum Schema „Schema zur einfachen Durchführung einer einfachen Varianzanalyse“ kann man daher wie folgt weiter rechnen:

Sutra	=		=	10800
SQ-Total	=		=	11441 – 10800	=	642
SQ-Prüfglieder	=		=	11130 – 10800	=	330
SQ-Fehler	=	642 – 330	=	312
FG-Total	=	N – 1	=	12 – 1	=	11
FG-Prüfglieder	=	K – 1	=	4 – 1	=	3
FG-Fehler	=	11 – 3	=	8

Die Ergebnisse kann man in eine Varianztabelle eintragen, die MQ-Werte errechnen und den F-Test durchführen (siehe Tabelle 17).

Tabelle 17: Varianztabelle für einen Versuch mit 4 Prüfgliedern nach der einfachen Varianzanalyse

	SQ	FG	MQ	F-Wert
Total	642	11
Prüfglieder	330	3	110,0	2,82
Fehler	312	8	39,0

Ein Blick auf Tabelle 15, die F-Tabelle, zeigt, dass der errechnete Wert von 2,82 nicht signifikant ist. Der Grenzwert für 3 und 8 FG liegt bei 4,07. Daher ist es durchaus möglich, dass alle Prüfglieder der gleichen Grundgesamtheit entstammen. Es darf demnach noch nicht behauptet werden, dass sich die Unterschiede in der Fütterung der Tiere auf die durchschnittliche tägliche Zunahme ausgewirkt haben.

Mit der abgegebenen Auswertung sind aber die Möglichkeiten der Varianzanalyse nicht erschöpft. Unter der Voraussetzung, dass es für den Versuch ein biologisch sinnvolles Konzept der Blockbildung gibt und dass der Versuch als Blockversuch angelegt wurde, darf man bei den Daten aus Tabelle 16 die Zeilensummen bilden. Man erhält so eine weitere Komponente der Variabilität, die zusätzlich von der SQ-Total subtrahiert werden kann und oft zu einer Reduzierung von SQ-Fehler führt. Hier ergibt sich:

Zeilensummen:	100, 116, 144		1
SQ – Blocks:		=	11048 – 10800	=	248
SQ – Fehler:	642 – 330 – 248	=	64

Stets ist es erforderlich, auch die Freiheitsgrade der Blockvarianz zu subtrahieren. Hier sind das 3 – 1 = 2. Nicht jede Blockbildung führt daher auch zu einer Verminderung von MQ – Fehler. Hier allerdings erhält man:

Das aber ist ein Wert, der viel kleiner ist als der, den man bei der Auswertung nach der einfachen Varianzanalyse erhält.

Tabelle 18: Varianztabelle für einen Versuch mit 4 Prüfgliedern als Blockversuch (Daten aus Tabelle 16)

	SQ	FG	MQ	F-Wert
Total	642	11
Blocks	248	2	124,0
Prüfglieder	330	3	110,0	10,28
Fehler	64	6	10,7

Wie ein Vergleich der Tabellen 17 und 18 zeigt, war bei unserem Beispiel die Auswertung als Blockversuch durchaus erfolgreich, denn der F-Wert hat sich mehr als verdreifacht. Zwar liegt, wie Tabelle 15 zeigt, die Signifikanzschwelle jetzt bei 4,76, dennoch sind durch die erhebliche Verminderung von MQ-Fehler die Unterschiede zwischen den Prüfgliedern signifikant geworden.

Was heißt „biologisch sinnvolles Konzept der Blockbildung“? Nicht in jedem Fall ist die Variabilität innerhalb der Stichproben rein zufällig bedingt. Bei Tierversuchen können z.B. Unterschiede in der genetischen Konstitution der Tiere eine Ursache sein. Wenn es möglich wäre, nur Tiere des gleichen Genotyps zu verwenden, wäre die Variabilität innerhalb der Prüfglieder vermutlich viel geringer. Auch wenn man z.B. bei Schweinen nur Wurfgeschwister verwenden könnte, wäre diese sicherlich vermindert. – Oft geht das schon deshalb nicht, weil zu viele Tiere benötigt werden. Es gibt aber zahlreiche Möglichkeiten zur Blockbildung, auch bei Tierversuchen. Es geht immer darum, die einander ähnlichen Tiere gleichmäßig über den Versuch zu verteilen, so dass auf jedes Prüfglied gleich viele jeder Gruppe kommen. Die Verrechnung als Blockversuch setzt aber voraus, dass bei der Versuchsplanung entsprechende Maßnahmen durchgeführt wurden und dass dies auch bei der Ordnung der Daten in Tabelle 16 Berücksichtigung fand. Man darf also nur dann den Versuch als Blockversuch verrechnen, wenn alle in einer Zeile stehenden Daten von einander ähnlichen Tieren stammten.

Bei der Bildung von Blöcken wird nicht selten die Fehlervarianz vermindert. Bei gegebener Zahl an Wiederholungen lassen sich dann bereits weniger ausgeprägte Differenzen statistisch sichern. Bei gegebenen Differenzen benötigt man entsprechend weniger Wiederholungen zur Erzielung eines bestimmten Signifikanzgrades.

Falls bei der Auswertung eines Versuches mit mehr als 2 Prüfgliedern ein Signifikanz anzeigender F-Wert errechnet wurde, erhebt sich die Frage, welche Differenzen signifikant sind. Um das zu prüfen, gibt es verschiedene Verfahren. Hier soll nur der multiple t-Test besprochen werden.

Für den multiplen t-Test muss man zunächst die Fehlervarianz errechnen, und zwar nach der folgenden Formel:

Außerdem benötigt man die Prüfgliedmittel, die zweckmäßigerweise gleich der Größe nach geordnet werden. Hier erhält man:

D = 24

B = 27

C = 31

A = 38

Demnach kann man für jede Differenz t-Werte errechnen, z.B.:

Bei der Beurteilung dieser t-Werte ist zu beachten, dass die Freiheitsgrade der Fehlervarianz verwendet werden dürfen. Hier sind das 6 und somit liegt die Signifikanzgrenze bei 2,45.

Eine elegante Möglichkeit zum Einsatz des multiplen t-Testes besteht in der Errechnung der Grenzdifferenz GD. Man erhält:

(33)

wobei t_0,05 der in der t-Tabelle für 5% Irrtumswahrscheinlichkeit aufzusuchende Grenzwert ist. Somit erhält man hier:

Alle Differenzen, die größer sind als diese Grenzdifferenz, sind dann signifikant.

Der multiple t-Test war früher sehr beliebt. Es lässt sich aber zeigen, dass er nur unter bestimmten Bedingungen zu unverzerrten Schätzungen des Signifikanzgrades von Prüfglieddifferenzen führt. Stets ist es bedeutsam, dass der Versuchsansteller alle Vorkenntnisse über die in einem bestimmten Versuch zu erwartende Rangfolge der Prüfgliedmittel berücksichtigt.

Auswertung faktorieller Versuche

Mithilfe von Versuchen, wie sie bisher besprochen wurden, lässt sich stets nur eine einzige Frage prüfen. Daher wird auch empfohlen, alle anderen Einflussfaktoren möglichst konstant zu halten. Mit dem Fortschritt der Wissenschaften führt dies immer häufiger zu einer ärgerlichen Einschränkung der Aussagemöglichkeiten. Streng genommen ist ja eine signifikante Differenz nur unter den Bedingungen des betreffenden Versuchs statistisch gesichert. Diese Bedingungen sind aber oft sehr spezifisch, bisweilen sogar nicht mehr reproduzierbar. In der Regel möchte der Versuchsansteller aus seinen Resultaten praktisch brauchbare Schlussfolgerungen ziehen. Beispielsweise ist es wenig interessant, welches Medikament sich in einem Versuch als bestes erwiesen hat, wenn man daraus nicht ableiten darf, dass dieses auch für die Praxis empfohlen werden kann. Um solchen Unzulänglichkeiten entgegentreten zu können, werden faktorielle Versuche durchgeführt und entsprechend ausgewertet. Sie bekommen schnell wachsende Bedeutung.

Wir wollen die spezifische Varianzanalyse für einfache faktorielle Versuche an dem bereits bekannten Beispiel besprechen. Dazu müssen wir jetzt annehmen, dass sich die 4 Prüfglieder in bestimmter Weise gruppieren lassen. Beispielsweise so, dass es sich um 2 unterschiedliche Futtermittel X und Y handelt, die einmal mit und einmal ohne einen Zusatzstoff verabreicht wurden, das wäre dann ein 2 x 2 – Versuch. Für dessen Auswertung muss man die Prüfgliedsummen wie folgt in eine „Zwei-Wege-Tafel“ einordnen:

Futtermittel	X		Y
Mit Zusatz	(A)	114	(B)	81	195
Ohne Zusatz	(C)	93	(D)	72	165
		207		153	360

Die Erweiterung der varianzanalytischen Auswertung besteht in der Zerlegung der SQ-Prüfglieder in ihre Komponenten. Bei 3 FG gibt es auch 3 Komponenten: Futtermittel, Zusatz und Interaktion oder Wechselwirkung. Zur Durchführung der Analyse errechnet man aus den oben bereits angegebenen Randsummen weitere SQ-Werte und erhält:

SQ-Futtermittel:	=	=	11043 – 10800	=	243
SQ-Zusatzstoffe:	=	=	10875 – 10800	=	75
SQ-Interaktion	=	=	330 – 243 – 75	=	12

Es ist üblich, diese Komponenten in die Varianztabelle so einzugliedern, wie es Tabelle 19 zeigt.

Tabelle 19: Varianztabelle für einen 2 x 2 – Versuch als Blockversuch (Daten aus Tabelle 16)

	SQ	FG	MQ	F-Werte
Total	642	11
Blocks	248	2	124,0
Prüfglieder	330	3	110,0	10,28
Futtermittel	243	1	243,0	22,71
Zusatzstoffe	75	1	75,0	7,01
Interaktion	12	1	12,0	1,12
Fehler	64	6	10,7

Bitte beachten Sie, dass die Komponenten der SQ-Prüfglieder nur 1 Freiheitsgrad haben. Die Signifikanzgrenze liegt deshalb bei 5,99. Dennoch sind die Komponenten „Futtermittel“ und „Zusatzstoffe“ als signifikant zu bezeichnen. Daraus könnte man folgern: Man darf annehmen, dass Futtermittel X besser ist als Y und dass sich auch die Vergabe des Zusatzstoffes positiv ausgewirkt hat. Da die Interaktion nicht signifikant ist, muss man vorläufig annehmen, dass sich der Zusatz bei beiden Futtermitteln gleich gut auswirkt.

Neu an der Auswertung dieses faktoriellen Versuches ist vor allem der Begriff der Wechselwirkung. Dahinter steht ein sogenanntes additives Modell, welches besagt, dass man, falls eine Behandlung A ein Plus von 5 erzeugt und Behandlung B ebenfalls, für die Kombination beider Behandlungen ein Plus von 5 + 5 = 10 zu erwarten hat, die Addition beider Wirkungen. Jede Abweichung von diesem additiven Verhalten erzeugt eine Interaktion. Bei unserem Beispiel verbessert der Zusatzstoff die Wirkung von Futtermittel X von 93 auf 114, also um 21, dagegen steigert er die Wirkung von Y nur von 72 auf 81, also um 9 Einheiten. Die Differenz der Differenzen: 21 – 9 = 12 ist für die SQ-Interaktion verantwortlich, die aber hier nicht signifikant ist.

Ergänzende Bemerkungen

In diesem Kapitel wurde von den verschiedenen Möglichkeiten zur Durchführung biometrischer Tests bei Messwerten lediglich die Prüfung der Differenz zwischen Stichprobenmittel behandelt, weil dies der Vergleich ist, der die größte praktische Bedeutung hat. Abschließend sollen einige ergänzende Bemerkungen zum Testen gegeben werden.

Die Prüfung der Differenz zwischen Stichprobenmitteln bei Messwerten entspricht gewissermaßen dem Homogenitätstest bei Häufigkeiten. So etwas wie einen Anpassungstest, also die Prüfung der Differenz zu Erwartungswerten, benötigt man, wenn es für ein bestimmtes Merkmal einen so genannten Normalwert gibt und geprüft werden soll, ob das Mittel einer Stichprobe davon abweicht.

Man kann den Normalwert mit gewissen Einschränkungen als arithmetisches Mittel einer Grundgesamtheit ansehen, denn er wurde aus einer sehr großen Stichprobe errechnet. Um zu prüfen, ob sich das Mittel einer Stichprobe davon signifikant unterscheidet, muss man errechnen und dann einen t-Wert nach folgender Formel:

(34)

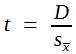
Bitte beachten Sie, dass man zur Prüfung der Signifikanz den Grenzwert für n – 1 Freiheitsgrade in der t-Tabelle ablesen muss.

Stichproben brauchen sich nicht nur im Mittel zu unterscheiden, sondern können auch in ihrer Standardabweichung bzw. in ihrer Varianz voneinander abweichen. Um solche Differenzen zu prüfen, kann man ebenfalls den F-Test verwenden. Ein Blick auf die F-Tabelle zeigt uns aber, dass die zufällige Streuung von Varianzen bei kleinen Stichproben erheblich ist. Wenn nämlich für je 4 Freiheitsgrade im Zähler und Nenner als Grenzwert für 5%-ige Irrtumswahrscheinlichkeit 6,39 zu finden ist, dann bedeutet das nichts anderes, als dass die Varianzen von Stichproben im Umfang 5 sich erst dann signifikant unterscheiden, wenn die eine größer als das 6,39-fache der anderen ist.

In dem in Tabelle 11 angegebenen Beispiel wurde und errechnet. Dividiert man durch , so erhält man einen F-Wert, und zwar:

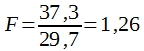
Dieser Wert ist also durchaus nicht signifikant. Erst wenn:

oder

wäre, dürfte man folgern, dass sich die Standardabweichungen der beiden Stichproben signifikant unterscheiden.

Vor der Durchführung eines biometrischen Tests muss man stets sorgfältig überlegen, was getestet werden soll und darf. Das ist gleichbedeutend mit der Forderung, die Null-Hypothese sorgfältig zu formulieren. Für alle Beispiele dieses Kapitels ging es um die Prüfung der Frage, ob die Mittel von Stichproben „verschieden“ sind oder nicht. Nicht selten gibt es gewisse Informationen über die vermutliche Rangfolge der Prüfgliedmittel schon vor der Durchführung des Versuches. Man weiß bereits, dass eine bestimmte Behandlung nicht schlechter sein kann als eine andere, es ist nur noch nicht sicher, ob sie besser ist. Man spricht in diesem Fall von einer einseitigen Fragestellung, und beim biometrischen Test geht es um die Errechnung einer einseitigen Überschreitungswahrscheinlichkeit.

Wegen der Symmetrie der Normalverteilung ist die einseitige Überschreitungswahrscheinlichkeit halb so groß wie die zweiseitige. Deshalb braucht man keine besonderen Tabellen, sondern lediglich die Werte für 2 ^. 5% = 10%, 2 ^. 1% = 2% und 2 ^. 0,1% = 0,2% in der t-Tabelle. Die Werte für 10% wurden in Tabelle 14 mit angegeben. Wenn also bekannt wäre, dass das Mittel von Stichprobe A nicht niedriger sein kann als das von Stichprobe B in Tabelle 11, wäre die Signifikanzgrenze bei t = 186 und die Differenz daher signifikant.

Da man bei einseitiger Fragestellung eher zu signifikanten Differenzen kommt als bei zweiseitiger, ist es verlockend, einseitig zu testen. Bitte beachten Sie jedoch, dass dazu eindeutig sichergestellt sein muss, dass echte Abweichungen wirklich nur in einer Richtung auftreten können. Man muss daher fordern, dass diese Richtung bereits vor der Durchführung des betreffenden Versuches zweifelsfrei definiert werden konnte.

Beim t-Test und bei der Varianzanalyse handelt es sich um sogenannte parametrische Tests. Streng genommen sind sie nur gültig, wenn die Messwerte in den Stichproben normalverteilt sind. Eine weitere Forderung, die erfüllt werden muss, ist die der Varianzgleichheit in allen Stichproben. Stets muss man daher überlegen, ob man die genannten Tests verwenden darf.

Wir hatten die Normalverteilung als Grenzwert der Binomialverteilung kennengelernt. Daraus könnte man folgern, dass wir dann eine Normalverteilung erwarten dürfen, wenn die Variation innerhalb der Stichproben rein zufällig ist. Dem steht jedoch entgegen, dass die Quadrate oder Kuben von Messwerten eine rechts schiefe Verteilung ergeben müssen, wenn die Orginalwerte selbst normalverteilt sind. Das bedeutet z.B., dass die Körpergewichte von Tieren eigentlich nicht normalverteilt sein können, wenn ihre Schulterhöhen einer Normalverteilung folgen.

Die Unsicherheit über das Vorliegen einer Normalverteilung hat dazu geführt, dass manche Biometriker den so genannten parameterfreien Verfahren generell den Vorzug geben. Die Geschlossenheit und Übersichtlichkeit des Systems der parametrischen Verfahren hat große Vorzüge und man sollte sie verwenden, solange dies möglich ist.

Erfreulicherweise hat sich gezeigt, dass der t-Test und der F-Test bei normaler Anwendung robust sind. Das heißt, dass ihre Ergebnisse in guter Annäherung gültig bleiben, bis die Abweichungen von der Normalverteilung krass sind. Weiterhin hat sich gezeigt, dass die Abweichungen von Normalität und Varianzgleichheit selten krass werden, wenn die relative Streuung innerhalb eines Versuches nicht sehr hoch ist, wenn z.B. alle Einzelwerte zwischen 70 und 130% des Generalmittels liegen. Schließlich hat sich gezeigt, dass bei kleinen Stichproben die Zufallsstreuung der Varianzen so groß ist, dass echte Differenzen in der Regel darin untergehen. Es ist außerdem stets möglich, durch nichtlineare Transformationen, beispielsweise durch die Verwendung von Logarithmen an Stelle der Originalmesswerte, krasse Abweichungen von der Normalverteilung zu beseitigen.

PDF-Version: Pruefung_Messwerte