Maßzahlen zur quantitativen Beschreibung von Befunden

Stichproben und Merkmale

Die Frage, wie schwer sind Äpfel, lässt sich im wissenschaftlichen Sinne nicht dadurch beantworten, dass man lediglich einen einzelnen Apfel auf die Waage legt. Jeder weiß, dass das Gewicht von Äpfeln ebenso variiert, wie andere Messungen und Beobachtungen an Lebewesen. Man bezeichnet das als „natürliche Variabilität der Organismen“. Es ist daher erforderlich, mehrere Messungen durchzuführen.

Die Bestimmung des Durchmessers eines möglichst gleichförmigen Gegenstandes mithilfe eines Messschiebers demonstriert diese Aussage anhand eines technischen Gegenstandes. Der Versuch veranschaulicht die Problematik. Messungen sind also stets mit einer Messunsicherheit behaftet (Lapidar: Wer misst, misst Mist!).

In der Regel möchte man aus den Untersuchungsergebnissen gewisse verallgemeinernde Schlussfolgerungen ziehen. Dann sind die Individuen, an denen die Messungen oder Zählungen durchgeführt wurden, oder die Werte selbst als Stichprobe zu bezeichnen. Allerdings meint der Chemo-/Biometriker, wenn er von einer „Stichprobe“ spricht, stets eine repräsentative Auswahl aus einer „Grundgesamtheit“, die ihrerseits möglichst exakt definiert sein muss.

Was da im Einzelfall gemessen oder gezählt wurde, bezeichnet man als „Merkmal“. Wichtig ist, dass präzis definierte Messvorschriften vorgegeben werden. Die Merkmale unterscheiden sich voneinander hinsichtlich ihres Variationstyps und müssen deshalb in unterschiedlicher Weise biometrisch bearbeitet werden.

Die früher übliche Differenzierung nach qualitativ und quantitativ variierenden Merkmalen ist ungenügend. Man gliedert sie besser nach dem metrischen Niveau ihrer Variationsskala und unterscheidet folgende Skalentypen:

	Skalentyp	Merkmal	Beispiel
1	Nominalskala	Es gibt eine begrenzte Zahl an Ausprägungsstufen, die keine natürliche Ordnung aufweisen	Rasse, Geschlecht, Blutgruppe
2	Ordinalskala	Es gibt eine natürliche Ordnung für die Stufen	Noten
3	Intervallskala	Die Ausprägungsstufen sind äquidistant, haben aber keinen natürlichen Nullpunkt	Körpertemperatur
4	Rationalskala	Es gibt einen natürlichen Nullpunkt, aber keine natürliche Einheit	Körpergewicht, Alter
5	Absolutskala	Es gibt auch eine natürliche Einheit	Ferkelzahl, Zahl der Früchte eines Baumes

Mit dem Anstieg des metrischen Niveaus der Skala von 1 nach 5 sinkt die Menge der zulässigen Transformationen (Umformungen), dagegen steigt die Menge der sinnvollen biometrischen Maßzahlen. Beispiel der Blutgruppe (nominalskaliertes Merkmal):

Von Original image: Schneider00 vectorization: Eigenes Werk – Eigenes Werk, Gemeinfrei, Link

Es gibt 4 eindeutig unterscheidbare Ausprägungsstufen. Eine natürliche Ordnung gibt es nicht. Die Bildung von Mittelwerten im Sinne einer mittleren Blutgruppe in einer ethnischen Gruppe oder einer Bevölkerung ist sinnfrei.

Allerdings darf dabei auch die Präzision der Messung beziehungsweise die Anzahl der in einer Stichprobe realisierten Stufen nicht außer Acht gelassen werden. Zu wenig Stufen hat man in der Regel, wenn die Messungen ohne Messinstrumente nur mittels unserer Sinne durchgeführt wurden. Man spricht dann von Bonituren und bonitiert beispielsweise den Geschmack des Apfels, die Blattfarbe von Pflanzen oder die Färbung eines Indikators im Laufe einer Titration.

Beispiel manuelle Säure-Base-Titration mit Phenolphthalein als Indikator:

Von Luigi Chiesa – Draw by Luigi Chiesa, Gemeinfrei, Link

Durch die Festlegung geeigneter Randbedingungen lässt sich das Ausmaß der erreichbaren Messunsicherheit minimieren. Der Farbumschlag von farblos nach rosa/pink beziehungsweise die Entfärbung mit einer für 45 Sekunden anhaltenden Rosafärbung könnte Gegenstand einer Bonitur sein. Eine Karte mit der Referenzfarbe, ein zuvor durchgeführter Test auf die Unterscheidbarkeit zweier Referenzfarben, Anforderungen an die mindeste Lichtqualität (Helligkeit, Farbqualität z.B. neutralweiß …), Farbsehvermögen der beurteilenden Person und weitere Festlegungen dienen zur Verbesserung der Vergleichbarkeit von Prüfergebnissen. Zudem beeinflussen die verwendete Apparatur die erzielbare Präzision und die Qualität des Titrationsmittels und viele weitere Faktoren das Ergebnis.

Häufigkeiten

Bei nominalskalierten Merkmalen sowie immer dann, wenn die Zahl der in einer Stichprobe realisierten Ausprägungsstufen zu gering ist, zählt man, wie häufig die verschiedenen Stufen auftreten. Um die Ergebnisse mit anderen Zählwerten vergleichen zu können, werden relative Häufigkeiten errechnet, indem man die Anzahl der Beobachtungen der betreffenden Merkmalsklassen durch die Gesamtzahl dividiert. Wird anschließend mit 100 multipliziert, erhält man Prozentzahlen. Da die Aussagekraft von Relativwerten von der wirklichen Anzahl der Beobachtungen abhängt, ist diese unbedingt in der Ergebnisangabe zu nennen. Werden gleichzeitig die Zählwerte für mehr als ein Merkmal ermittelt, ist es zweckmäßig, die Häufigkeit in ein mehrdimensionales Schema einzuordnen, das als Kontingenztafel bezeichnet wird. Die Randsummen ergeben dann die Häufigkeiten für die einzelnen Merkmale.

Das arithmetische Mittel

Bitte nehmen Sie an, dass die Frage nach dem Geburtsgewicht von Kälbern zu folgenden Messergebnissen geführt hat (in kg):

47

31

42

44

39

Dies ist eine eher kleine Stichprobe, man könnte sich darauf beschränken, die Einzelwerte mitzuteilen. Es ist aber üblich und mindestens bei größeren Stichproben erforderlich, den Befund durch charakteristische Kennzahlen, durch biometrische Maßzahlen, zu beschreiben. Die in den Zahlen steckende Information soll dadurch deutlich und bequem erkennbar werden. Ursachen für kleine Stichproben können in Kostenerwägungen, Verfügbarkeit von Material liegen. Die Qualität von Prüfungen steigt zudem nicht linear mit der Zahl der Wiederholungsuntersuchungen.

Mittelwerte sind eine Klasse von biometrischen Maßzahlen. Bei richtiger Auswahl der Stichproben beschreiben sie die Lage des Zentrums der Grundgesamtheit, für die die verallgemeinernden Schlussfolgerungen gelten sollen. Der bekannteste und wichtigste Mittelwert ist das arithmetische Mittel.

Für alle Maßzahlen benötigt man eine Rechenvorschrift. Hinsichtlich des arithmetischen Mittels könnte diese lauten: Bilde die Summe der Messwerte und dividiere das Ergebnis durch die Anzahl.

Eine einfache Rechenvorschrift, wie die für das arithmetische Mittel, kann man auch verbal ausdrücken. Oft wird das sehr umständlich, und es ist daher zweckmäßig, eine Formel anzugeben. Für jede Formel benötigt man Symbole. Für die Berechnung des arithmetischen Mittels in der Formeldarstellung benötigte Symbole:

	∑	Summenzeichen
	xi	Einzelwert
	n	Anzahl
		arithmetisches Mittel

Die Formel lautet dann:

(1) 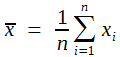Dies ist eine mathematisch korrekte Formel. Solange sie lediglich als Gedankenstütze dienen soll, ist es zweckmäßig, eine vereinfachte Schreibweise zu verwenden, mindestens für Nichtmathematiker. Diese lautet:

(2)

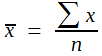
Die obigen Formeln sind Grundformeln. Solche Grundformeln zeigen besonders anschaulich, was im Prinzip zu rechnen ist. Wenn man wirklich rechnen muss, sind sie häufig unbequem. Man verwendet nach Möglichkeit spezielle Berechnungsformeln, die an die besonderen Bedingungen des betreffenden Falles angepasst sind und dazu führen, dass Sie

a) mit der Rechnung schnell fertig werden,

b) nicht so leicht Fehler machen.

Für kleine Stichproben gibt es beim arithmetischen Mittel allerdings keine Berechnungsformel. Aus den angegebenen Geburtsgewichten errechnet man daher nach Formel (2):

47
31
42
44
39

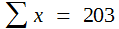
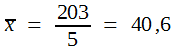
Zahlen fallen nicht vom Himmel!

In der Praxis beginnt die Arbeit nicht mit der Rechnung, sondern mit der Planung der Untersuchung, der Durchführung der Messung und der Protokollierung der Messergebnisse. Für große Stichproben, d. h. wenn mehr als 30 Messungen geplant sind, sollte man besondere Maßnahmen zur Organisation der Eintragung der Einzelergebnisse vornehmen. Da dies zum Fachgebiet der Dokumentation gehört, soll hier kurz erwähnt werden, dass man die „Daten“ zunächst in eine Urliste einträgt. Um rückführbare, qualitätssichere Daten zu erhalten, muss die Urliste formalen Mindestansprüchen genügen (Datum, Projektbezug, Bearbeiter …). In der Mehrzahl der Fälle, ist es zweckmäßig, schon im Verlauf der Arbeit eine primäre Verteilungstafel in Form einer Strichliste anzulegen.

Dies gilt vor allem für stetig variierende Merkmale, wie z. B. das Körpergewicht, bei denen es keine natürlichen Klassen gibt. In der primären Verteilungstafel werden die Originalwerte zu künstlichen Klassen zusammengefasst. Entsprechend der Formel:

(3)

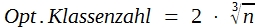
ergibt sich eine optimale Klassenzahl. n ist dabei die Zahl der beabsichtigten Messungen. Diese optimale Klassenzahl ist lediglich eine Faustzahl.

Das Verfahren wird in Schema A demonstriert. – Wenn man eine Anzahl von Messungen durchgeführt hat (vielleicht 15 – 20), errechnet man aus der Differenz zwischen dem größten und kleinsten Wert die vorläufige Variationsbreite. Aus dieser erhält man einen Schätzwert für die optimale Klassenbreite. Man muss dann noch die Klassengrenze festlegen und dabei beachten, dass:

a) die Klassengrenzen eindeutig sind,

b) die Klassenmitten möglichst glatte Zahlen ergeben,

c) es am Rand keine offenen Klassen gibt.

Für die Berechnung des arithmetischen Mittels aus einer zu Klassen zusammengefassten großen Stichprobe gibt es mehrere Verfahren. Eines davon, das Multiplikationsverfahren, möchte ich Ihnen erläutern.

Man verwendet die Formel:

(4)

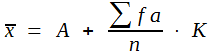
in dieser Formel bedeuten:

	A	ein frei wählbares Arbeitsmittel
	f	die Frequenzen, d. h. die Anzahl der Werte in den betreffenden Klassen
	a	die Abweichungen von A in Klassenbreiten
	K	die gewählte Klassenbreite

Beginn Schema A	Organisation eines Verfahrens zur Durchführung einer einfachen Erhebung
1	Urliste (Anfang) Der geplante Stichprobenumfang ist n =  150 Die Urliste enthält natürliche Zahlen, also Zahlen ohne Nachkommastellen.
2	Vorläufige Variationsbreite (größter minus kleinster Wert der ersten Messungen)	71 – 29 = 42
3	Geschätzte definitive Variationsbreite circa	50 – 55
4	Optimale Klassenzahl Bei n = 150
5	Optimale Klassenbreite	50 : 11 = 4,6
6	Gewählte Klassenbreite	K = 5
7	Gewählte untere Grenzen der Klassen, um glatte Zahlen für die Klassenmitten zu bekommen	27,5; 32,5; 37,5; ……..

8. Strichliste

Klassen	Mitten	Striche	Frequenzen
27,5 – 32,5	30	II	2
32,5 – 37,5	35	II	2
37,5 – 42,5	40	IIII IIII IIII	15
42,5 – 47,5	45	IIII IIII IIII IIII IIII IIII IIII III	38
47,5 – 52,5	50	IIII IIII IIII IIII IIII IIII IIII IIII I	41
52,5 – 57,5	55	IIII IIII IIII IIII IIII IIII IIII	34
57,5 – 62,5	60	IIII IIII IIII	15
62,5 – 67,5	65	II	2
67,5 – 72,5	70	I	1

Ende Schema A

Wie im Folgenden das Schema B zeigen wird, eignet sich ein frei wählbares Klassenmittel, das etwa in der Mitte der Verteilung liegt, als Arbeitsmittel. Anschließend werden die Abweichungen von A in Klassenbreiten berechnet und unter Beachtung des Vorzeichens mit den dazugehörigen Frequenzen multipliziert. Diese f ^. a werden summiert, wobei man zweckmäßigerweise zuerst die negativen und positiven Werte getrennt addiert. Aus A und der errechneten Summe sowie nach Multiplikation mit K, erhält man dann .

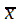Die Formel ist so geartet, dass verhältnismäßig kleine Zwischenergebnisse entstehen und die Wahrscheinlichkeit für Rechenfehler bei manueller Auswertung minimiert wird. Die nach Formel (4) errechneten Mittel sind an sich nicht exakt. Liegt aber die Zahl der Klassen nicht wesentlich unter dem nach Formel (3) errechneten Optimum, sind sie stets genau genug.

Für alle biometrischen/chemometrischen Maßzahlen gibt es auch eine „optimale Genauigkeit“. Sie sind keinesfalls genauer anzuben. 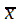erreicht diese bei kleinen Stichproben, wenn es um eine Stelle genauer angegeben wird, als die einzelnen Messwerte, bei größeren Stichproben, also falls n>30 sind 2 zusätzliche Stellen angebracht. Erst bei Stichproben mit n>3000 ist 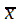um 3 Stellen genauer anzugeben. Allerdings sollte die letzte der angegebenen Stellen immer gerundet sein.

Die optimale Genauigkeit des arithmetischen Mittels ergibt sich aus der Tatsache, dass alle Messwerte ungenaue Zahlen sind. Der 1. Messwert in Schema A ist zum Beispiel nicht exakt 29, sondern eine ungenaue Zahl im Intervall 28,5 bis 29,5. Diese Ungenauigkeiten wirken sich auf das Mittel aus. Sie führen dazu, das zusätzliche Stellen keinen Informationswert haben, sodass die zu präzise Angabe eines Mittels an „biometrische Hochstapelei“ grenzt.

Wegen der natürlichen Variabilität der Organismen lohnt es sich auch nicht, zu präzis zu messen. Nur ausnahmsweise sind mehr als 3 zählende Stellen angebracht. Die Begründung ergibt sich aus den Fehlerfortpflanzungsgesetzen (siehe Abschnitt Link folgt).

Mithilfe der Differenzialrechnung lässt sich beweisen, dass die Summe der Abweichungen von x=0, die Summe der Abweichungsquadrate von diesem Punkt ein Minimum ist. (Link auf Ergänzung und Beweis).

Schema B: Berechnung des arithmetischen Mittels nach dem Multiplikationsverfahren (Daten aus Schema A)

	x	f	a	fa
	30	2	-4	-8
	35	2	-3	-6
	40	15	-2	-30
	45	38	-1	-38
					-82
A->	50	41	0
	55	34	+1	34
	60	15	+2	30
	65	2	+3	6
	70	1	+4	4
					74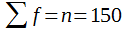

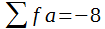
Definitive Berechnung nach Formel (4):

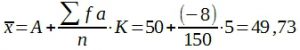
Zentralwert und Dichtemittel

Das arithmetische Mittel ist nur eine von zahlreichen deskriptiven biometrischen Maßzahlen. Die wichtigsten Klassen solcher Maßzahlen sind:

1. Mittelwerte

2. Streuungsmaße

3. Deformationsmaße

4. Assoziationsmaße

Bei jeder dieser Klassen gibt es verschiedene Maßzahlen. Somit ist das arithmetische Mittel nur einer von mehreren Mittelwerten. Warum der arithmetische Mittelwert der wichtigste ist ergibt sich im Anschluss an die Erläuterung von zunächst mit mindestens zwei weiteren Mittelwerten, mit dem Zentralwert (=x_z) und dem Dichtemittel (=x_D).

Der Zentralwert, auch Median genannt, ist der „mittelste“ Wert einer der Größe nach geordneten Zahlenmenge. Diese verbale Definition ist einprägsamer als jede Formel

1. Ordne die eingangs angegebenen 5 Geburtsgewichte der Kälber nach ihrer Größe:

31

39

42

44

47

2. Wähle die „mittelste“ Zahl.

Wie ersichtlich, ist 42 der in der Mitte stehende Wert, sodass wir ohne weitere Rechenarbeit niederschreiben können: X_Z=42. So einfach geht das allerdings nur bei einer ungeraden Anzahl an Einzelwerten.

3. Ist n eine gerade Zahl, gibt es keinen mittleren Wert. Man errechnet hilfsweise das arithmetische Mittel der beiden in der Mitte stehenden Zahlen.

Bei größeren Stichproben ist es mühevoll, die Zahlen der Größe nach zu ordnen. Hier ist es üblich, sie zu Klassen zusammenzufassen. Man berechnet dann die „Eintauchtiefe“ des mittleren Wertes in die zentrale Klasse, d. h. in die Klasse, in der dieser Wert liegt. Eine dazu geeignete Berechnungsformel lautet:

(5)

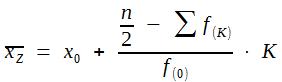
In der Formel werden folgende Symbole erstmalig benutzt:

	=	Untere Grenze der zentralen Klasse
	=	Anzahl der Werte unterhalb der zentralen Klasse
	=	Anzahl der Werte in der zentralen Klasse

Zur Berechnung des Zentralwerts werden zunächst jeweils die Frequenzen (Häufigkeiten) der Strichlistenklassen von der kleinsten Klasse beginnend bis zu der individuell betrachteten Klasse addiert. Mit den Daten aus Schema A ergeben sich für die Zwischensummen zur Berechnung des Zentralwerts:

 

Klassenmitten	f
30	2	2
35	2	4
40	15	19
45	38	57
50	41	98
55	34	132
60	15	147
65	2	149
70	1	150

Demnach liegt der Zentralwert in der Klasse mit der Mitte 50 und der unteren Grenze 47,5. Die Anzahl der Werte bis zur Klassengrenze beträgt 57. „n / 2“ ist 75. Nach Einsetzen in Formel (5) ergibt sich:

 

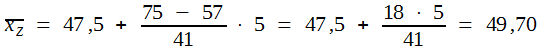
Diese Berechnung geht von einer gleichmäßigen Verteilung der einzelnen Werte in der zentralen Klasse aus. Der Zentralwert liegt dann bei unserem Beispiel um 18 / 41 von der unteren Grenze der zentralen Klasse entfernt.

Dichtemittel

Das Dichtemittel soll anzeigen, wo in der Verteilung die Werte am dichtesten liegen. Daraus folgt zunächst, dass seine Berechnung nur bei großen Stichproben sinnvoll ist und dass vorher die Einzelwerte zu Klassen zusammengefasst werden müssen. Man könnte als X_D einfach die Mitte der Klasse angeben, in der die meisten Einzelwerte liegen, jedoch ist es üblich, die Frequenzen in den beiden Nachbarklassen mitzuberücksichtigen. Demnach kommt man zu folgender Formel:

(6)

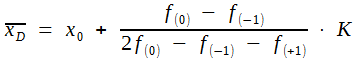
f(-1)	Anzahl der Werte in der Klasse unterhalb der zentralen Klasse
f(+1)	Anzahl der Werte in der Klasse oberhalb der zentralen Klasse

Aus den in Schema A angegebenen Werten das Dichtemittel ergibt sich:

f(0) = 41

f(-1) = 38

f(+1) = 34

und demnach:

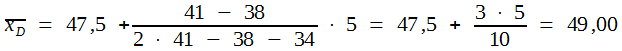
Gesichtspunkte zur Verwendung verschiedener Mittelwerte

Alle biometrischen Maßzahlen haben einen irgendwie begrenzten Anwendungsbereich. Wer sie bewusst falsch anwendet, begeht eine statistische Fälschung. Es genügt deshalb nicht, zu wissen, wie man eine bestimmte Zahl errechnet. Man muss auch lernen, wo und wie man sie korrekt verwendet.

Bei den Mittelwerten gilt es zunächst zu prüfen, ob es überhaupt sinnvoll ist, einen von ihnen zu errechnen. Danach kommt es darauf an, den richtigen zu verwenden. Die erste Frage ist so zu beantworten, dass Mittelwerte nur bei intensiven, quantitativen und genügend stetigen Merkmalen gebildet werden dürfen.

Die Begriffe „quantitativ“ und „stetig“ wurden bereits erläutert. Hinsichtlich der Bezeichnung „intensiv“ ist zu sagen, dass im Gegensatz dazu ein extensives Merkmal, bei dem zum Beispiel bei der Bevölkerungszahl verschiedener Gebiete, die Summe den Befund besser beschreibt als der Mittelwert. Bezüglich der Begriffe quantitativ und qualitativ wäre zu betonen, dass sich artmäßige Merkmale bisweilen durch Bewertung in quantitative umwandeln lassen und dann ein Mittelwert berechnet werden darf. Bei diesen diskreten Merkmalen kommt es auf die Stufenzahl an. Sind mehr als 5 Stufen vorhanden, ist die Errechnung eines Mittelwertes in der Regel sinnvoll.

Falls man bei einem Merkmal Mittelwerte errechnen darf, kommt man zur zweiten Frage: Welcher Mittelwert ist der beste? Aus den in Schema A angegebenen Daten ergaben sich folgende Mittelwerte:

XA = 49,73

XZ = 49,70

XD= 49,0

Das sind nahezu gleiche Ergebnisse. Eine solche Übereinstimmung ergibt sich stets, wenn wie in Schema A auch gezeigt, die Verteilung der Einzelwerte etwa symmetrisch ist. Dagegen würden sich die drei Mittelwerte deutlich unterscheiden, wenn die Einzelwerte eine schiefe Verteilung ergeben.

Tabelle 1: 3 Stichproben mit n = 100 und X_A = 50

 

Klasse	Anzahl der Werte
	1	2	3
30	1	–	–
35	5	1	2
40	9	15	44
45	20	37	18
50	32	19	9
55	17	11	6
60	10	6	5
65	4	4	3
70	2	3	2
75	–	2	2
80	–	1	3
85	–	1	1
90	–	–	2
95	–	–	2
100	–	–	1

In Tabelle 1 sind die Daten von 3 Stichproben aufgelistet, deren Mittel gleich sind. Dagegen sind die Werte nur bei Stichprobe 1 nahezu symmetrisch verteilt, während die Verteilung bei Stichprobe 2 deutlich und bei 3 sehr schief ist. Errechnet man aus diesen Zahlenkolonnen die 3 Mittelwerte, so erhält man:

 

	XA	XZ	XD
Stichprobe 1	50,00	49,84	49,72
Stichprobe 2	50,00	47,09	45,25
Stichprobe 3	50,00	43,61	40,59

Die 3 Mittelwerte unterscheiden sich um so stärker, je schiefer die Verteilung ist.

Deutlich schiefe Verteilungen kommen in der Natur nicht selten vor. In vielen Fällen liegt dann nur der Zentralwert an der Stelle, wo man aufgrund einer grafischen Darstellung einen Mittelwert erwarten würde. Dann ist nur X_Z der Mittelwert, der das Ergebnis der Untersuchung objektiv widerspiegelt, daher kann man ihn als eine repräsentative Maßzahl ansehen.

Beispiel 1: Die Frage nach dem mittleren verfügbaren Einkommen lässt sich je nach Art Mittelung unterschiedliche Ergebnisse zu. Der große Unterschied dieser Mittelwerte ergibt sich aus der Art der Einkommensverteilung.

Beispiel 2: Asymmetrische Verteilungen sind in Biologie und Physik nicht selten. Die Poisson-Verteilung gehört zu diesen asymmetrischen Verteilungen. Die Energieverteilung der Betastralung (ß-Strahlung) im radioaktiven Zerfall folgt der Poisson-Verteilung.

Die Tatsache, dass X_A und X_Z bei symmetrischen Verteilungen nahezu übereinstimmen und bei schiefen X_Z die repräsentativere Maßzahl ist, verleitet zu dem Schluss, den Zentralwert als den wichtigsten Mittelwert anzusehen. Dieser Schluss ist voreilig, weil es neben der Repräsentativität einer Maßzahl als zweites Kriterium für ihre Güte noch die Präzision gibt.

Aus Stichproben errechnete Mittelwerte sollen möglichst gute Schätzwerte für das Zentrum der betreffenden Grundgesamtheit sein. Zieht man aus einer Gesamtheit mit bekanntem Zentrum zahlreiche Stichproben und errechnet von jeder X_A und X_Z, so zeigt sich, dass die X_A-Werte im Durchschnitt etwas besser mit dem Mittelwert der Gesamtheit übereinstimmen als die Zentralwerte. Das arithmetische Mittel ist demnach der präzisere Schätzwert.

Die Präzision solcher Schätzwerte für den Mittelwert einer Gesamtheit lässt sich natürlich verbessern, indem man die Stichproben vergrößert. Es zeigt sich, dass X_A aus Stichproben von 10 Einzelwerten Schätzwerte etwa gleicher Präzision liefert wie X_Z aus einem Stichprobenumfang von 16. Man bezeichnet das arithmetische Mittel deshalb als eine effiziente Maßzahl. Demnach ist zu folgern:

1. Bei etwa symmetrischen Verteilungen ist das arithmetische Mittel unbedingt zu bevorzugen.

2. Bei Verteilungen mit zunehmender Schiefe verwende man das arithmetische Mittel, solange das Ergebnis einigermaßen repräsentativ ist, sonst den Zentralwert.

Das Dichtemittel hat nur eine geringe Präzision. Seine Verwendung beschränkt sich deshalb auf spezielle Probleme, vor allem da, wo nach sogenannten Normalwerten gesucht wird, beispielsweise nach dem normalen Heiratsalter oder dem normalen Blutdruck. Es handelt sich dabei ausschließlich um große Stichproben. Der Vorteil von X_A gegenüber X_Z vermindert sich, wenn die Stichprobe „Ausreißer“, d. h. falsche Messwerte enthält, jedoch bleibt X_A in der Praxis fast immer präziser als der Zentralwert.

Variationsmaße

Mittelwerte sind zwar die wichtigsten Maßzahlen zur biometrischen Beschreibung einer Stichprobe, sie sind aber allein nicht ausreichend, weil sie nichts über das Ausmaß der Variation, der Streuung der Einzelwerte aussagen. Um zu einer vollständigeren Beschreibung der Verteilung zu kommen, müssen sie durch Streuungsmaße ergänzt werden.

Ein sehr einfaches und anschauliches Maß für die Streuung in einer Stichprobe ist die Variationsbreite (= VB), die Differenz zwischen dem größten und dem kleinsten Wert.

(7)

VB = X_(max) – X_(min)

Da diese Variationsbreite lediglich durch die Position der beiden extremen Einzelwerte bestimmt wird, kann sie keine effiziente Maßzahl sein. Die effizienteste Maßzahl für die Beschreibung der Streuung ist die so genannte Standardabweichung (=s). Es handelt sich um die Quadratwurzel aus der mittleren quadratischen Abweichung. Die Grundformel lautet:

(8)

Tabelle 2 zeigt die Berechnung der Standardabweichung nach dieser Grundformel bei einer kleinen Stichprobe.

Es ist üblich, Mittelwert und Standardabweichung gemeinsam anzugeben, und zwar in der Form X_A ± s, wobei beide Zahlen mit der gleichen Genauigkeit errechnet und niedergeschrieben werden sollten. Demnach hätten Sie zur biometrischen Beschreibung der Werte aus Tabelle 2 Folgendes auszugeben: 40,6 ± 6,1. Manchmal ist es überflüssig, die Quadratwurzel zu ziehen. Man bezeichnet das Quadrat der Standardabweichung als mittleres Abweichungsquadrat oder als Varianz.

Tabelle 2: Berechnung der Standardabweichung nach der Grundformel

 

x
47	6,4	40,96
31	-9,6	92,16
42	1,4	1,96
44	3,4	11,56
39	-1,6	2,56

Bei Formel (8) ist merkwürdig, dass durch n – 1 dividiert werden muss. Der Grund dafür ist, dass die Varianz einer Stichprobe ein unverzerrter Schätzwert der Varianz der betreffenden Grundgesamtheit sein soll. Diese Unverzerrtheit ist ein weiteres Kriterium für die Güte einer biometrischen Maßzahl. Hier bedeutet sie, dass die Erwartungswerte der mittleren Abweichungsquadrate verschieden großer Stichproben aus der gleichen Grundgesamtheit alle gleich groß und ebenso groß wie die Varianz der Gesamtheit selbst sein sollten.

Man bezeichnet das Mittel der Gesamtheit mit µ, ihre Standardabweichung mit σ. Wenn µ bekannt wäre, könnte man x – µ bilden. In der Praxis ist das niemals der Fall, und man muss hilfsweise X_A errechnen und die x – x_A bilden. Da ihre Quadratsumme ein Minimum ist, ist sie kleiner als die Summe der (x – µ)². Demzufolge ist Σ(x-x_A)² verzerrt. Es lässt sich zeigen, das die Verzerrung im Durchschnitt durch die Division durch n – 1 korrigiert wird.

Die Frage, warum man bei der Division durch n – 1 unverzerrte Stichprobenvarianzen erhält, wird gern dahin gehend beantwortet, dass man sagt, einer der Stichprobenwerte ist durch die Berechnung des arithmetischen Mittels festgelegt, Man müsse stets durch die Zahl der variablen Größen, durch die Freiheitsgrade dividieren. Diese Definition ist zwar eine gute Gedankenstütze, aber kein Beweis.

Bei der Varianz beziehungsweise der Standardabweichung ist es bereits in kleinen Stichproben zweckmäßig, eine spezielle Berechnungsformel zu verwenden. Die Grundformel hat demnach nur didaktischen Wert. Eine geeignete Berechnungsformel für kleine Stichproben lautet:

(9)

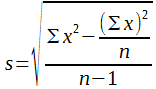
Der Vorteil dieser Formel besteht darin, dass man die Abweichungen der Einzelwerte von X_A nicht zu bilden braucht. Nach Formel (9) errechnet man sich die Standardabweichung aus den in Tabelle 2 angegebenen Daten, wie in Tabelle 3 ersichtlich.

Tabelle 3: Berechnung der Standardabweichung nach der Berechnungsformel

x	x2
47	2209
31	961
42	1764
44	1936
39	1521

Formel (9) enthält zahlenmäßig verhältnismäßig große Zwischenergebnisse. Ohne Rechenhilfsmittel entstehen dabei leicht Rechenfehler. Es ist daher zweckmäßig, eine lineare Transformation vorzunehmen. Das heißt, von jedem Einzelwert wird ein bestimmter Betrag subtrahiert, ein Arbeitsmittel. Man erhält dann:

und kommt zu folgender Formel:

(10)

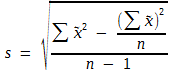
Bei den Werten aus Tabelle 2 empfiehlt sich die Subtraktion von 30. Wie dann zu rechnen ist, zeigt Tabelle 4.

Tabelle 4: Berechnung der Varianz nach Transformation der Ausgangsdaten

x
47	17	189
31	1	1
42	12	144
44	14	196
39	9	81

Damit ergibt sich die gleiche Standardabweichung mit s=6,1 wie aus den nichttransformierten Daten.

Bei größeren Stichproben ist es zweckmäßig, s nach folgender Formel zu errechnen:

(11)

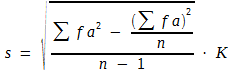
Dies setzt die Transformation der großen Stichprobe in eine Strichliste voraus. Formel (11) ist eine Erweiterung des Multiplikationsverfahrens zur Berechnung des arithmetischen Mittels, das durch Formel (4) definiert wurde. Im nachfolgenden Schema wird die Berechnung anhand der bereits in Schema A angegebenen Daten erläutert. Wie ersichtlich ist, kann man die für die Berechnung des arithmetischen Mittels benötigten Zwischenwerte verwenden und braucht sie lediglich durch eine weitere Zeile, die fa² zu ergänzen.

Schema C: Berechnung der Standardabweichung nach dem Multiplikationsverfahren (Daten aus Schema A)

Basisrechnungen falls A = 50 gewählt wurde:

	x	f	a	f a		f a2
	30	2	-4	-8		32
	35	2	-3	-6		18
	40	15	-2	-30		60
	45	38	-1	-38		38
A->	50	41	0			–
	55	34	1	34		34
	60	15	2	30		60
	65	2	3	6		18
	70	1	4	4		16
				-8

Definitve Berechnung nach Formel (11)

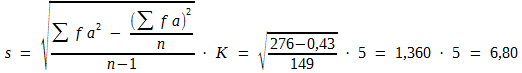
Die nach Formel (11) errechnete Standardabweichung ist dann verzerrt, wenn die Messwerte zu künstlichen Klassen zusammengefasst wurden. Die Verzerrung lässt sich korrigieren, wenn man 1/12 mal K² von der Varianz subtrahiert (Shepphard’sche Korrektur). Für das in Schema C angegebene Beispiel erhält man:

Während das arithmetische Mittel eine unmittelbar anschauliche Größe ist, bedarf es einiger Hinweise zur Veranschaulichung der Standardabweichung. Zwar besteht kein unmittelbarer Zusammenhang zwischen der Variationsbreite und der Standardabweichung, doch ist diese fast immer kleiner als 6 s. Das bedeutet, dass nahezu alle Einzelwerte zwischen x_A – 3s und x_A + 3s liegen. In der Regel findet man zirka 5% der Werte außerhalb von x_A – 2s und x_A + 2s und rund ein Drittel außerhalb von x_A – 1s und x_A + 1s. Die Varianz ist nicht invariant zu linearen Transformationen und deshalb zur biometrischen Beschreibung einer Verteilung ungeeignet. Die Standardabweichung ist zwar als Variationsmaß am präzisesten, aber ihre Präzision sehr viel geringer ist als die von x_A.

Aus s leitet sich der Variationskoeffizient ab. Er ist die durch das arithmetische Mittel dividierte Standardabweichung und wird folglich mit s% bezeichnet. Man benötigt einen solchen Relativwert, wenn man die Variabilität verschiedener Merkmale miteinander vergleichen möchte, beispielsweise die des Körpergewichtes mit der des Gewichtes einzelner Organe.

Während die Berechnung einer Maßzahl für die Streuung stets eine wichtige Ergänzung zur Mittelwertbildung bringt, ist es fraglich, ob es sich lohnt, weitere Maßzahlen zu errechnen. Bekannt sind Maße für Schiefe (=S) und Exzess (=E).

Das präziseste Maß für die Schiefe erhält man aus den 3. Potenzen der Abweichungen von x_A. Man dividiert durch die 3. Potenz der Standardabweichung und erhält so eine unbekannte Maßzahl. Das hat den Vorteil, dass solche Schiefeziffern aus verschiedenen Stichproben direkt vergleichbar sind. Bei ausgeprägt schiefen Verteilungen ist S entweder größer als 1 (=rechtsseitige Schiefe) oder kleiner als -1 (= linksseitige Schiefe). Schiefeziffern, die um weniger als 0,5 von 0 abweichen, sind unbedeutend. Von den 3 Stichproben in Tabelle 1 errechnet sich für die erste eine Schiefe von 0,11; für die zweite von 1,42 und für die dritte ein Wert von 1,68.

Der Exzess ist ein Maß für die Form des Gipfels. Er ist positiv, wenn die Verteilung hochgipfelig und langschwänzig ist; er ist negativ, wenn sie breitgipfelig und kurzschwänzig ausfällt. Man errechnet den Exzess aus den vierten Potenzen der Abweichungen von x_A.

PDF-Version dieses Kapitels: Masszahlen_Biometrie