Zufallsexperimente und Ereigniswahrscheinlichkeiten
Schon im täglichen Leben begegnet man immer wieder Wahrscheinlichkeiten und Zufällen. Genau genommen sind nahezu alle Erkenntnisse der Wissenschaft nur Wahrscheinlichkeitsaussagen. Durch die Wahrscheinlichkeitsrechnung wird versucht, die „Gesetzmäßigkeiten des Zufälligen“ zu erfassen. Man geht dabei gern von sogenannten Zufallsexperimenten aus, die möglichst einfach sind und zugleich als Modell für andere, nicht so einfach zu demonstrierende und zu erläuternde Experimente dienen sollen.
Das allereinfachste Experiment ist der Talerwurf (Eurowurf). Die geworfene Münze fällt zu Boden und zeigt entweder Zahl oder Symbol. Das Ergebnis ist durchaus kausal bedingt, denn es ist abhängig vom Anfangszustand, der Wurfgeschwindigkeit, der Rotationsgeschwindigkeit und weiteren ähnlichen Bedingungen. Da man ohne besonderes Training die einzelnen Komponenten nicht konstant halten kann, ist das Ergebnis nicht vorhersagbar, jedenfalls wenn man, was hier stets vorausgesetzt wird, die Münze hoch genug wirft.
Das Ergebnis eines einzelnen Wurfes bezeichnet man als stochastisches Ereignis. Beim Talerwurf gibt es nur zwei mögliche Ereignisse, Zahl oder Symbol – oder wie auch immer der „Taler“ auf den beiden Seiten gekennzeichnet sein mag. Man sagt, dass diese beiden Ereignisse den ganzen Ereignisraum abdecken. In anderen Zufallsexperimenten, z. B. beim Würfeln, gibt es mehr als zwei mögliche Ereignisse, bisweilen sogar unendlich viele. Alle hier zu besprechenden Zufallsexperimente haben jedoch einen endlichen Ereignisraum.
Als Zufallsexperiment kann man ebenso wie einen einzelnen Wurf auch eine Serie von mehreren gleichzeitig oder nacheinander ausgeführten Würfen bezeichnen, z. B. eine Serie von 10 Würfen. Im Verlauf einer solchen Serie könnte beispielsweise siebenmal rot und dreimal weiß aufgetreten sein. (Bei einem rot-weißen Taler). Dann sagt man, die relative Häufigkeit für rot sei:
![]()
In Gedanken kann die Serie immer weiter wachsen, unendlich groß werden. Falls dieses Experiment mit einem idealen Taler (d. h. mit einem idealen Taler (d.h. Mit einem homogen aufgebauten und gleichgeformten) durchgeführt wurde und falls sichergestellt ist, dass das Ergebnis aller Würfe zufällig ist, besteht kein Grund zur Annahme, dass die eine Seite häufiger nach oben kommen sollte als die andere. Die Ereigniswahrscheinlichkeit für die beiden allein möglichen Ereignisse wird als „gleich“ angenommen. Folglich gilt:
![]()
und
![]()
Hieraus ergibt sich zugleich, dass man die Gesamtwahrscheinlichkeit aller möglichen Ereignisse gleich 1 setzt. Ereigniswahrscheinlichkeiten müssen daher stets zwischen 0 und 1 liegen, wobei p = 1 für das sichere Ereignis, p = 0 für ein unmögliches Eintreffen eines Ereignisses x steht.
Eine allseits befriedigende Definition für den Begriff der Wahrscheinlichkeit gibt es noch nicht. Für den vorliegenden Zweck genügt es, die Wahrscheinlichkeit für das Eintreffen eines Ereignisses x zu definieren:
![]()
Dies ist die stochastische Definition der Wahrscheinlichkeit.
Die Frage, ob man beim Werfen mit dem Taler im Verlauf einer großen Serie von Würfen wirklich zu Ergebnissen kommt, die dem erwarteten Wert p = 0,5 nahe kommen, hat im vorvergangenen Jahrhundert viele Statistiker beschäftigt. Heute ist es so, dass man so einfache Probleme durch Nachdenken lösen kann. Die experimentelle Überprüfung von Zufallsmethoden durch Simulation ist aber durchaus modern. Man bezeichnet so etwas als Monte-Carlo-Methode und bedient sich dazu eines Rechners. Die Ergebnisse einer Simulation von 100000 Würfen zeigt die folgende Tabelle. Wie ersichtlich, stimmt die Häufigkeit für die Gesamtzahl aller Würfe sehr gut mit p = 0,5 überein.
Simulation des Talerwurfs durch eine EDV-Anlage (50mal 2000 Würfe)
| rot | weiß | rot | weiß | rot | weiß | rot | weiß | rot | weiß |
|---|---|---|---|---|---|---|---|---|---|
|
990 |
1010 |
986 |
1014 |
982 |
1018 |
1021 |
979 |
1021 |
979 |
|
1034 |
966 |
1016 |
984 |
988 |
1012 |
991 |
1009 |
1030 |
970 |
|
1031 |
969 |
1011 |
989 |
1023 |
977 |
1002 |
998 |
1014 |
986 |
|
997 |
1003 |
966 |
1034 |
960 |
1040 |
976 |
1024 |
949 |
1051 |
|
969 |
1031 |
1022 |
978 |
1000 |
1000 |
1004 |
996 |
1015 |
985 |
|
1002 |
998 |
1009 |
991 |
997 |
1003 |
1013 |
987 |
980 |
1020 |
|
1018 |
982 |
999 |
1001 |
1004 |
996 |
990 |
1010 |
1013 |
987 |
|
984 |
1016 |
1026 |
974 |
1006 |
994 |
963 |
1037 |
993 |
1007 |
|
976 |
1024 |
1024 |
976 |
1007 |
993 |
971 |
1029 |
977 |
1023 |
|
982 |
1018 |
1031 |
969 |
996 |
1004 |
987 |
1013 |
1028 |
972 |
Summe aller roten: 49974
Summe aller weißen 50026
Rechenregeln für das Rechnen mit Wahrscheinlichkeiten
Der Einführung weiterer Begriffe der Wahrscheinlichkeitsrechnung dient ein Zufallsexperiment, bei dem mehr als 2 Ereignisse eintreffen können. Hier sei es das Würfeln mit einem regulären Würfel. – Es gibt dabei sechs mögliche Ereignisse, die alle gleich wahrscheinlich sind und zusammen den gesamten Ereignisraum überdecken. Es ist daher zu formulieren:
![]()
Es geht um den Begriff der zusammengesetzten Wahrscheinlichkeit, also z. B. um die Beantwortung der Frage, wie wahrscheinlich es ist, mit einem Würfel eine Zahl <3, also eine 1 oder eine 2 zu werfen. – Man versteht sofort, dass dies gleich der Summe der beiden Ereigniswahrscheinlichkeiten sein muss.
Um die Frage etwas allgemeiner beantworten zu können, ist es üblich und nützlich, Symbole und Begriffe der Mengenlehre zu verwenden. Dort spricht man bekanntlich von Grundmengen und Teilmengen. Der ganze Ereignisraum ist dann einer Grundmenge äquivalent, die sich in 6 gleich große Teilmengen, den einzelnen Wahrscheinlichkeiten, aufgliedert. Beim Würfeln schließen sich die Ereignisse gegenseitig aus, denn man kann nicht zugleich eine 1 und eine 2 werfen. Demnach liegen die Teilmengen sauber getrennt nebeneinander. Sie haben keine gemeinsamen Elemente.
|
p(1) |
p(2) |
p(3) |
p(4) |
p(5) |
p(6) |
|---|---|---|---|---|---|
|
|
Man kann daher formulieren:
(12)
![]()
(13)
![]()
Beim Würfeln mit 2 Würfeln, schließen sich die Ereignisse nicht mehr gegenseitig aus. Das entspricht der Situation der Mengenlehre, in der Teilmengen gemeinsame Elemente haben, sich also partiell überlagern. Man erhält hier zunächst:
(14)
![]()
wobei – wie noch erläutert wird – die Aussage: die Ereignisse schließen sich nicht gegenseitig aus, nicht ausreicht, damit Formel 14 gültig ist.
Am interessantesten ist die Antwort auf die Frage nach der Wahrscheinlichkeit, wenigstens mit einem von beiden Würfeln eine 1 zu werfen. Die richtige Antwort lautet:
(15)
![]()
Die Richtigkeit dieser Formel erklärt am besten die folgende Abbildung:
|
6′ |
||||||
|---|---|---|---|---|---|---|
| 5′ | ||||||
| 4′ | ||||||
| 3′ | ||||||
| 2′ | ||||||
| 1′ | ||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
Der Ereignisraum wurde hier in je 6 horizontale und vertikale Streifen unterteilt, die den Ereigniswahrscheinlichkeiten des einen und des anderen Würfels entsprechen. Man erhält 36 Felder. Je 6 davon entsprechen der Wahrscheinlichkeit, mit einem der Würfel eine 1 zu werfen. Da eines der beiden Felder in beide Streifen fällt, muss man von der Summe der beiden Streifen ihr Produkt subtrahieren, weil sonst das Feld 1,1′ doppelt gezählt würde, und erhält demnach:
![]()
Ändert man das 2-Würfel-Modell in der Weise, dass man fordert, nicht gleichzeitig, sondern nacheinander zu würfeln, dann gilt die Annahme der bedingten Wahrscheinlichkeit. Hier soll dann z. B. die Frage beantwortet werden, wie groß dann die Wahrscheinlichkeit ist, beim zweiten Wurf eine 1 zu werfen, wenn schon bekannt ist, dass beim ersten eine 1 geworfen wurde. Leicht ist einzusehen, dass dieser Wert unverändert gleich bleibt, also unabhängig vom Ergebnis des ersten Wurfes ist. Es ist üblich, dies durch folgende Gleichung anzugeben:
![]()
Für weitere Überlegungen ist es zweckmäßig, ein anderes Modell zu verwenden. Unter den natürlichen Zahlen gibt es solche, die durch 2 teilbar sind, andere sind durch 4 teilbar und noch andere durch 5. Auf die Frage nach dem Ereignisraum gibt es folgende Antworten:
Hier geht es allerdings um bedingte Wahrscheinlichkeiten, also z.B. um die Frage: Wie groß ist p(5), wenn bekannt ist, dass die ausgewählte Zahl durch 2 teilbar ist?
Man erhält:
![]()
und ebenso:
![]()
Im Gegensatz dazu:
![]()
denn alle durch 4 teilbaren Zahlen sind gerade Zahlen und die Hälfte der geraden Zahlen ist durch 4 teilbar. Man sagt: Die Teilbarkeit durch 5 ist von der Teilbarkeit von 2 und ebenso von der Teilbarkeit durch 4 stochastisch unabhängig und formuliert allgemein:
Die Ereignisse A und B sind dann stochastisch unabhängig, wenn:
(16)
![]()
und zugleich gilt
![]()
Bitte merken: Die Formeln (14) und (15) gelten nur, wenn die betreffenden Ereignisse stochastisch unabhängig sind, das ist aber beim Würfeln mit zwei Würfeln der Fall.
Die Frage nach der stochastischen Unabhängigkeit führt zu wichtigen Anwendungsmöglichkeiten für das Rechnen mit Wahrscheinlichkeiten. Man prüft an praktischen Problemen, ob die Wahrscheinlichkeit für das Auftreten einer Kombination zweier Ereignisse so groß ist, wie sie nach Formel (14) oder (15) sein sollte. Ist das nicht der Fall, darf man schließen, dass die Ereignisse nicht voneinander unabhängig waren. Das ist oft ein Ansatzpunkt für wichtige fachliche Schlussfolgerungen.
Bitte beachten Sie, dass man bei Problemen aus der Praxis nur selten die wahren Ereigniswahrscheinlichkeiten kennt. In der Regel kann man nur aus den gegebenen Stichproben Häufigkeiten errechnen. Dies mindert nur gelegentlich den Wert der Rechnungen, führt aber, wie später noch näher erläutert wird, zu wichtigen Schlussfolgerungen, die man aus den Ergebnissen ziehen darf.
Wahrscheinlichkeitsverteilungen
Vielfach ist das exakte Ergebnis eines Zufallsexperimentes uninteressant. So möchte z. B. ein Spieler vor allem wissen, mit welcher Wahrscheinlichkeit er zu einer bestimmten Augensumme kommt. Nicht so wichtig ist es für ihn, welche verschiedenen Ereigniskombinationen dort hinführen und welche Einzelwahrscheinlichkeiten diese haben. Betrachtet man in dieser Weise das 2-Würfel-Modell, so zeigt sich zunächst, dass die Wahrscheinlichkeiten für verschiedene Augensummen ungleich sind. Man erhält:
2 Augen nur in der Kombination 1 / 1
3 Augen durch die Kombinationen 1 / 2 und 2 / 1
4 Augen durch die Kombinationen 1 / 3, 2 / 2 und 3 / 1
und so fort.
Da die Einzelkombinationen alle gleich wahrscheinlich sind, erhält man hier, wie die folgenden Abbildungen zeigen eine Dreiecksbildung für die Augensummen.
Tabelle: Mögliche Kombinationen zweier Würfelpunkte zur Erzielung möglicher Augensummen
-
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
1′
2′
3′
4′
5′
6′
Tabelle: Wahrscheinlichkeit für das Werfen bestimmter Augensummen mit 2 Würfeln
-
1
1/36
2/36
3/36
4/36
5/36
6/36
2
2/36
3/36
4/36
5/36
6/36
5/36
3
3/36
4/36
5/36
6/36
5/36
4/36
4
4/36
5/36
6/36
5/36
4/36
3/36
5
5/36
6/36
5/36
4/36
3/36
2/36
6
6/36
5/36
4/36
3/36
2/36
1/36
1′
2′
3′
4′
5′
6′
|
6/36 |
x |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
5/36 |
x |
x |
|||||||||
|
4/38 |
x |
x |
|||||||||
|
3/36 |
x |
x |
|||||||||
|
2/36 |
x |
x |
|||||||||
|
1/36 |
x |
x |
|||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
x-Achse: Augensummen; y-Achse: Wahrscheinlichkeit im 2-Würfelmodell
So zustande gekommene Verteilungen werden als Wahrscheinlichkeitsverteilungen bezeichnet. Bisweilen ist es zweckmäßiger, die Wahrscheinlichkeiten der verschiedenen Augensummen aufzuaddieren. Für das 2-Würfel-Modell ergeben sich:
Man bezeichnet eine derartige Verteilung als Summenfunktion der Wahrscheinlichkeiten.
Besonders einfach und zugleich besonders wichtig sind die Wahrscheinlichkeitsverteilungen, die aus Modellen mit Alternativmerkmalen, wie z. B. dem Talerwurfmodell resultieren. – Wirft man zwei Taler zugleich und setzt rot = p und weiß = q, dann ergibt sich nach den Regeln für das Rechnen mit Wahrscheinlichkeiten [Formel (14)]:
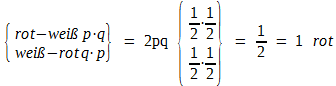
![]()
Das gleiche Ergebnis lässt sich aufgrund eines Binoms (p + q)2 mit p = q = 0,5 ausdrücken. Man erhält:
![]()
![]()
Wahrscheinlichkeiten, die so auf Alternativmerkmalen aufbauen, bezeichnet man deshalb als Binomialverteilungen. Beim Wurf mit 4 Talern kommt man mithilfe des Binoms zu folgenden Wahrscheinlichkeiten:
![]()
mit den Einzelgliedern:
![]()
![]()
![]()
![]()
![]()
Für größere Stichproben ist es zweckmäßiger, sich vorzustellen, dass man als Zufallsexperiment Kugeln aus einer Urne zieht, die 2 Sorten solcher Kugeln, z. B. rote und weiße enthält. Dann nämlich lässt sich das Experiment so abwandeln, dass die beiden Sorten nicht gleich häufig sind. Falls in der Urne 60% rote und 40% weiße Kugeln sind, würde man p = 0,6 und q = 0,4 setzen und für Stichproben vom Umfang 4 zu folgenden Ergebnissen kommen:
0,64 = 0,1296 für 4 rot
4 . 0,63 . 0,4 = 0,3456 für 3 rot
6 . 0,62 . 0,42 = 0,3456 für 2 rot
4 . 0,6 . 0,43 = 0,1536 für 1 rot
0,44 = 0,0256 für 0 rot
Die angegebenen Wahrscheinlichkeiten gelten als exakt nur dann, wenn entweder unbegrenzt viele Kugeln in der Urne sind oder die Kugel einzeln gezogen und nach dem Zug sofort wieder zurückgelegt werden. Ohne Zurücklegen kommt man bei endlicher Kugelzahl zu einer hypergeometrischen Verteilung.
Die Unterschiede zwischen Binomial- und der hypergeometrischen Verteilung sind nur dann beachtlich, wenn die Stichprobe nicht sehr viel kleiner ist als die Grundgesamtheit, also z. B. der Kugelvorrat in der Urne. Hat man nur je 3 rote und weiße Kugeln, dann ändert sich das Verhältnis nach dem 1.Zug stets von 0,5 auf 0,4; nach dem 2.Zug entweder auf 0,5 zurück oder auf 0,25 : 0,75. Somit erhält man bei einer Stichprobe von 3 Kugeln ohne Zurücklegen:
rot – rot – rot = 0,5 . 0,4 . 0,25 = 0,05
rot – rot – weiß = 0,5 . 0,4 . 0,75 = 0,15
und so fort.
Eine Gegenüberstellung der Wahrscheinlichkeitswerte dieser hypergeometrischen Verteilung mit der betreffenden Binomialverteilung finden Sie in Tabelle 6.
| Anzahl rot | Wahrsch. o. Zurücklegen | Wahrsch. m. Zurücklegen |
|---|---|---|
|
3 |
0,05 |
0,125 |
|
2 |
0,45 |
0,375 |
|
1 |
0,45 |
0,375 |
|
0 |
0,05 |
0,125 |
Wie ersichtlich, treten bei der hypergeometrischen Verteilung Extremwerte seltener, Werte in der Nähe des Zentrums häufiger auf. Eine typische hypergeometrische Verteilung ergibt sich aus der Ziehung der Lottozahlen.
Binomial- und hypergeometrische Verteilung sind nur zwei besonders markante Beispiele für theoretische Wahrscheinlichkeitsverteilungen, die sich von der Mengenlehre bei stochastischer Unabhängigkeit entwickeln lassen. In der Praxis hat man außerdem häufig mit empirischen Wahrscheinlichkeitsverteilungen zu tun. Sie basieren ausnahmslos auf Stichprobenergebnissen, sodass es sich streng genommen nur um Häufigkeitsverteilungen handelt. Je nach dem Umfang und der Repräsentativität der betreffenden Stichproben sind die angegebenen Einzelwahrscheinlichkeiten in ihrer Präzision recht unterschiedlich. Man sollte von einer empirischen Wahrscheinlichkeitsverteilung erst dann sprechen, wenn die angegebenen Werte aus sehr großen Stichproben mit einem Mindestumfang von 3000 Einzelbeobachtungen errechnet wurden.
Wahrscheinlichkeitsverteilungen in der Genetik
Die Genetik ist ein Zweig der biologischen Wissenschaften, in dem die Wahrscheinlichkeitsrechnung eine wesentliche Rolle spielt. Wenn man 2 genetisch differierende Pflanzen miteinander kreuzt, erhält man in der sogenannten F2 eine Aufspaltung, die einem Zufallsexperiment gleichzusetzen ist. Bei dominant – rezessivem Erbgang und Spaltung in nur einem Gen, wie z. B. bei der Kreuzung von rot blühenden mit weiß blühenden Erbsen ist p = 0,75, q = 0,25. Dies sind die Basiswahrscheinlichkeiten. Die Aufspaltung nach frei spaltenden Genen entspricht einer Binomialverteilung (p + q)2, wobei die mittlere Klasse aufgeteilt werden muss. Man erhält:
![]()
![]()
![]()
![]()
Biometrisch besonders interessant ist das „Verhalten von Genen in Populationen“. Hier sind die verschiedenen Keimzellklassen nicht gleich häufig. Wenn wir annehmen, dass in einer Population 80% der Keimzellen vom Typ A und 20% vom Typ a vorhanden sind, dann ergeben sich zufallsgemäßer Kombination folgende Wahrscheinlichkeiten:
A X A = 0,8 . 0,8 = 0,64
A X a = 0,8 . 0,2 = 0,16
a X A = 0,2 . 0,8 = 0,16
a X a = 0,2 . 0,2 = 0,04
A X a sind nicht unterscheidbar von a X A mit insgesamt 0,32
Dies ist dann ein Gleichgewichtszustand der Genotypen, der ohne äußere Einflüsse unverändert erhalten bleibt, weil daraus wiederum 80% A und 20% a Keimzellen entstehen. Nach seinem Entdecker bezeichnet man ihn als Hardy-Weinberg-Gesetz.
Eine wichtige Folgerung aus dem Hardy-Weinberg-Gesetz ist, dass bei seltenen rezessiven Genen der betreffende Phänotyp noch viel seltener in der Population auftritt. Wenn wir annehmen, dass q = 0,01, dann treten homozygot rezessive Individuen nur mit einer Wahrscheinlichkeit von q2 = 0,012 = 0,0001 auf. Derartige Verhältnisse haben wir in der Regel bei Erbkrankheiten, und man kann daraus eine relative Unwirksamkeit von Sterilisationsmaßnahme ableiten. Falls p = 0,99 und demnach q = 0,01, erhält man:
| p2 | = 0,992 | = 0,9801 | AA |
| 2pq | = 2 . 0,99 . 0,01 | = 0,0198 | Aa |
| q2 | = 0,012 | = 0,0001 | aa |
Nur die aa-Individuen sind als krank erkennbar und könnten sterilisiert werden. Im Beispiel sind das 1% aller a-Gene. 99% dieser Gene kommen dagegen nur „verdeckt“ in den Heterozygoten vor und bleiben demnach unerkannt. „Dank“ molekularbiologischer Techniken hat sich dies im Laufe der letzten Jahrzehnte geändert und damit setzt die ethische Diskussion erneut ein.
Erwartungswert und Varianz
Um Wahrscheinlichkeitsverteilungen beschreiben oder miteinander vergleichen zu können, berechnet man auch hier Maßzahlen wie und s. Mindestens bei theoretischen Wahrscheinlichkeitsverteilungen handelt es sich nicht um Stichproben sondern um eine Menge, die mit einer Grundgesamtheit vergleichbar ist. Daher bezeichnet man die Maßzahlen als Parameter. Außerdem ist es üblich, das arithmetische Mittel einer Wahrscheinlichkeitsverteilung als mathematische Erwartung zu bezeichnen und mit E zu symbolisieren. Wichtiger als die Standardabweichung ist hier die Varianz, die mit V bezeichnet wird. Bei Anpassung der im Kapitel 1 besprochenen Grundformel an die Besonderheiten einer Wahrscheinlichkeitsverteilung erhält man:
(17)
![]()
(18)
![]()
In Formel (18) darf nicht durch n-1 dividiert werden, weil es sich, wie erläutert wurde, nicht um Stichproben handelt. Allerdings wäre diese Division durch n-1 ohnehin nicht möglich, weil hier die Summe der pi = 1 ist. Die Berechnung von E und V für die auf dem Binom (0,5 + 0,5)4 basierende Verteilung (sie entspricht der Ziehung von 4 Kugel aus einer Urne mit gleich vielen roten und weißen Kugeln) zeigt Tabelle 7.
Tabelle 7: Berechnung von E und V bei einer Binomialverteilung mit p=q=0,5 und n=4 (xi=Anzahl rot)
| xi | pi | xipi | (xi – E) | (xi – E)2 pi |
|---|---|---|---|---|
|
4 |
0,0625 |
0,25 |
2 |
0,25 |
|
3 |
0,2500 |
0,75 |
1 |
0,25 |
|
2 |
0,3750 |
0,75 |
0 |
– |
|
1 |
0,2500 |
0,25 |
-1 |
0,25 |
|
0 |
0,0625 |
– |
-2 |
0,25 |
| E(x) = 2,00 | V(x) = 1,00 |
Demnach ist die mathematische Erwartung E = 2 rote Kugeln, und dieser Wert streut mit einer Varianz V = 1.
Bei empirisch ermittelten Wahrscheinlichkeitsverteilungen und auch bei der hypergeometrischen Verteilung muss man E und V in der angegebenen Weise berechnen. Nur für Binomialverteilungen lässt sich zeigen, dass einfacher zu handhabende Formeln eingesetzt werden können, nämlich:
(19)
E(x) = np
(20)
V(x) = npq
Für das in Tabelle 7 erläuterte Beispiel kann man daher auch wie folgt rechnen:
| E(x) | = np | = 4 . 0,5 | = 2 |
| V(x) | = npq | = 4 . 0,5 . 0,5 | = 1 |
Die vereinfachten Formeln sind vor allem dann wichtig, wenn es sich um Binomialverteilungen mit ![]() und größeren Werten für n handelt. So erhält man z. B. für ein Binom mit p = 0,8; q = 0,2 und n = 100 folgende Resultate:
und größeren Werten für n handelt. So erhält man z. B. für ein Binom mit p = 0,8; q = 0,2 und n = 100 folgende Resultate:
E(x) = 100 . 0,8 = 80
V(x) = 100 . 0,8 . 0,2 = 16
Bei Verwendung der Formeln (17) und (18) wäre hierzu eine recht umfangreiche Rechnung erforderlich.
Überschreitungswahrscheinlichkeiten und biometrische Tests
In Tabelle 8 finden Sie die Ereigniswahrscheinlichkeiten für die sich auf das Binom (0,5 + 0,5)16 aufbauende Binomialverteilung.
Tabelle 8: Ereigniswahrscheinlichkeiten bei der Binomialverteilung mit p = q = 0,5 und n = 16, z. B. Ziehen von 16 Kugel aus einer Urne mit gleich vielen roten und weißen Kugeln
| Anzahl rot | p |
|---|---|
|
16 |
0,00002 |
|
15 |
0,00024 |
|
14 |
0,00183 |
|
13 |
0,00854 |
|
12 |
0,02777 |
|
11 |
0,06665 |
|
10 |
0,12219 |
|
9 |
0,17456 |
|
8 |
0,19638 |
|
7 |
0,17456 |
|
6 |
0,12219 |
|
5 |
0,06665 |
|
4 |
0,02777 |
|
3 |
0,00854 |
|
2 |
0,00183 |
|
1 |
0,00024 |
|
0 |
0,00002 |
Eine solche Verteilung erwartet man, wenn aus einer Urne mit gleich vielen roten und weißen Kugeln Stichproben von je 16 Kugeln gezogen werden (mit zurücklegen). Die mathematische Erwartung ist hier E = 16 . 0,5 = 8 und – wie die Tabelle zeigt – ist das auch die Kugelzahl mit der größten Wahrscheinlichkeit. Andererseits ist p(18) aber nur 0,19638, so dass man 8 rote Kugeln noch nicht einmal bei jeder 5. Stichprobe erwarten darf.
Zur Lösung wichtiger biometrischer Probleme genügt es nicht, die Ereigniswahrscheinlichkeiten zu kennen. Man muss vielmehr wissen, wie häufig Abweichungen bestimmter Größe vom Erwartungswert überschritten werden. Man bezeichnet das als Überschreitungswahrscheinlichkeit und verwendet P (Probability) als Symbol. P ergibt sich demnach als Summe entsprechender Ereigniswahrscheinlichkeiten. In der Regel ist es zweckmäßiger, zunächst 1 – P, die Nichtüberschreitungswahrscheinlichkeit zu errechnen, d. h. die Ereigniswahrscheinlichkeiten der inneren Glieder zu addieren. Für die in Tabelle 6 angegebene Binomialverteilung errechnet sich P(1), die Wahrscheinlichkeit, dass die Abweichung vom Erwartungswert >1 ist, wie folgt:
![]()
oder bequemer:
![]()
also nach Tabelle 8:
P(1) = 1- (0,17456 + 0,19638 + 0,17456) = 1 – 0,54550 = 0,45450
In gleicher Weise kann man weitere Überschreitungswahrscheinlichkeiten errechnen und erhält:
P(1) = 0,4545
P(2) = 0,2101
P(3) = 0,0768
P(4) = 0,0213
P(5) = 0,0042
P(6) = 0,0005
Wie ersichtlich werden die Überschreitungswahrscheinlichkeiten mit der Vergrößerung des Intervalls schnell kleiner. P(6) = 0,0005 bedeutet, dass eine Abweichung vom Erwartungswert, die größer als 6 ist, bei der hier betrachteten Binomialverteilung nur 5-mal unter 10000 Fällen rein zufällig auftritt. Man kann daher sagen: „Es ist unwahrscheinlich, dass beim Binom (0,5 + 0,5)16 die Abweichung vom Erwartungswert 8 größer wird als 6.“ Da eine solche Binomialverteilung beim Ziehen von 16 Kugeln aus einer Urne mit gleich vielen roten und weißen zu erwarten ist, kann man ebenso gut sagen: Es ist unwahrscheinlich, dass wir als Ergebnis der Ziehung mehr als 14 oder weniger als 2 rote Kugeln bekommen. Dies ist eine Wahrscheinlichkeitsaussage. Sie ist mit einem Irrtumsrisiko behaftet.
Man bezeichnet eine Aussage, wie sie soeben gegeben wurde, als den Schluss von der Gesamtheit auf die Stichprobe, und wir wollen die logischen Schritte, die zu dieser Aussage führen, noch einmal einzeln aufführen:
- Gegeben sei eine Urne mit bekanntem Verhältnis an roten und weißen Kugeln, z. B. Verhältnis 1:1.
- Ich möchte eine Stichprobe ziehen und überlege mir, was dabei herauskommen könnte. Da es sich um ein Zufallsexperiment handelt, kann ich allerdings nicht voraussagen, welche Ereigniskombination ich erhalten werde.
- Ich kann nur voraussagen, dass es unwahrscheinlich ist, dass die Abweichung vom Erwartungswert größer sein wird als ein bestimmter Wert.
- Ziehe ich eine Stichprobe von 16 Kugeln, so kann ich voraussagen, dass es unwahrscheinlich ist, dass die Abweichung vom Erwartungswert größer als 6 sein wird, weil man ausrechnen kann, dass dann so große oder größere Abweichungen rein zufällig nur selten auftreten.
In der angewandten Wissenschaft hat man es viel häufiger mit einer Umkehrung des Problems zu tun. Die logischen Schritte lassen sich dann wie folgt formulieren:
- Es gibt so etwas wie eine Urne mit unbekanntem Verhältnis, jedoch eine Hypothese über deren Inhalt, z. B. eine begründete Vermutung, dass es sich um ein Verhältnis 1:1 handelt.
- Bekannt ist lediglich das Ergebnis einer Stichprobe.
- Es soll geprüft werden, ob die Hypothese über das Verhältnis der Kugeln in der Urne durch das Stichprobenergebnis widerlegt wird.
Man bezeichnet eine derartige Prüfung als einen statistischen oder biometrischen Test. Wir wollen zeigen, zu welchen Schlussfolgerungen man bei einem solchen Test kommt und dazu zwei verschiedene Stichprobenergebnisse verwenden:
| Ergebnis A | 15 weiße und 1 rote Kugel |
| Ergebnis B | 5 weiße und 11 rote Kugeln |
Man erhält aufgrund der Berechnung der Überschreitungswahrscheinlichkeit:
Stichprobenergebnis A: (15:1) E bei Hypothese 1:1 = 8 gefundene Abweichungen 7
Die Überschreitungswahrscheinlichkeit für Abweichungen < 6 ist hier nur P = 0,0005, also ist die Abweichung vom Erwartungswert so groß, dass man nicht mehr annehmen darf, sie sei rein zufällig aufgetreten. Damit ist die Hypothese widerlegt; es kann sich nicht um ein 1:1 Verhältnis in der Urne handeln.
Stichprobenergebnis B: (5:11) E ist wiederum 8 gefundene Abweichungen 3
Die Überschreitungswahrscheinlichkeit für die Abweichungen <2 ist 0,2101. So große Abweichungen treten demzufolge auch rein zufällig ziemlich häufig auf, und die Nullhypothese, dass es sich um ein 1:1 Verhältnis in der Urne handelt, wird nicht widerlegt.
Ich möchte Sie bitten, die beiden Formulierungen aufmerksam zu lesen. Man kann wie beim Stichprobenergebnis A mittels eines biometrischen Tests zwar beweisen, dass eine Theorie falsch sein muss (wobei bei der Wahrscheinlichkeitsaussage stets ein Irrtumsrisiko bleibt), man kann aber nicht umgekehrt beweisen, dass sie richtig ist. Liegt das Untersuchungsergebnis dicht am Erwartungswert, darf man allenfalls formulieren, dass die „Hypothese durch das Ergebnis des Experimentes vorläufig gestützt wird“. War es jedoch eine fachlich vollkommen unbegründete Hypothese, dann bekommt sie durch das Stichprobenergebnis keinen Wahrscheinlichkeitsgehalt. Nur wenn die Annahme biologisch sinnvoll war, darf man sie durch einen biometrischen Test überprüfen.
Die Überlegungen haben eine eminent praktische Bedeutung. Bitte nehmen Sie an, dass eine bestimmte Impfung bisher nur zu 80% erfolgreich ist. Sie glauben, eine Modifikation des Verfahrens gefunden zu haben, die zu besseren Erfolgen führt. Ein zum Beweis Ihrer Theorie durchgeführtes Experiment zeigt, dass Sie 85 Tiere mit, 15 Tiere ohne Erfolg behandelt haben. Dürfen Sie behaupten, dass Ihr Verfahren besser ist?
Im Grunde ist Ihr Experiment mit dem Modellversuch des Ziehens von Kugeln aus einer Urne identisch. Die geimpften Tiere können in der Regel als eine Stichprobe aufgefasst werden. Bei einer erwarteten Erfolgsquote von 80% erwartet man eine Binomialverteilung mit p=0,8 und q=0,2. Ihre Stichprobe brachte 85:15 als Ergebnis, und biometrisch formuliert lautet Ihre Frage nun: Ist es wahrscheinlich, dass aus einer Binomialverteilung mit p=0,8 Stichproben vom Umfang 100 gezogen werden, deren Abweichung vom Erwartungswert >4 ist?
Zur Durchführung des Tests sind zunächst die Ereigniswahrscheinlichkeiten für die 9 inneren Glieder des Binoms (0,8 + 0,2)100 zu errechnen, deren Abweichung vom Erwartungswert nicht größer als 4 ist. Ihre Summe gibt dann die Nichtüberschreitungswahrscheinlichkeit, und man erhält schließlich P, indem man diese Summe von 1 subtrahiert. Die Rechnung ergibt P = 0,2545, und das bedeutet, dass es nicht sehr unwahrscheinlich ist, dass so große Abweichungen rein zufällig auftreten. Die Hypothese, das modifizierte Impfverfahren sei besser, wird daher durch das Experiment nicht bewiesen, die Gegenhypothese, dass es nicht besser sei, demzufolge vorläufig gestützt.
Dass soeben erläuterte Prüfungsverfahren hat nicht nur im Rahmen der Biometrie eine zentrale Bedeutung, sondern darüber hinaus auch für die Gewinnung neuer wissenschaftlicher Erkenntnisse in den Naturwissenschaften. Nahezu alle Aussagen dort sind im Grunde solche Wahrscheinlichkeitsaussagen. Die zweckmäßigste Form des Vorgehens bei der Anwendung eines biometrischen Tests soll daher noch einmal programmatisch beschrieben werden.
- Es gibt eine Hypothese über das zu erwartende Ergebnis einer Untersuchung.
- Zur Prüfung der Hypothese wird ein Experiment durchgeführt.
- Es gibt gewisse Abweichungen zwischen Erwartung und Befund.
- Man nimmt provisorisch an, dass die Abweichungen nicht echt, sondern nur rein zufällig sind (Null-Hypothese).
- Es wird die Überschreitungswahrscheinlichkeit für ebenso große und größere Abweichungen errechnet.
- In Abhängigkeit vom numerischen Wert der errechneten Überschreitungswahrscheinlichkeit wird entweder die Hypothese abgelehnt oder vorläufig bestätigt.
Exakte und approximative Tests
Das im vorhergehenden Abschnitt erläuterte Verfahren zur direkten Berechnung der Überschreitungswahrscheinlichkeiten ist ein exakter biometrischer Test. Insbesondere bei größeren Stichproben ist der zur Durchführung eines solchen Tests erforderliche Rechenaufwand erheblich. Da es nicht Sinn der Biometrie ist, zu langwierigen Rechnungen Anlass zu geben, ist ein approximativer Test immer dann zu bevorzugen, wenn er ein genügend genaues Ergebnis liefert. Die logische Basis eines approximativen Tests zur Prüfung von Häufigkeiten liegt in der Tatsache, dass zwischen der Überschreitungswahrscheinlichkeit und einem „t-Wert“ eine bestimmte Beziehung besteht. Als t-Wert bezeichnet man die durch die Standardabweichung dividierte Differenz zwischen Erwartung und Befund:
![]()
Diese Beziehung, die Wahrscheinlichkeit also, mit der t eine bestimmte Größe erreicht, wurde errechnet und zu einer Tabelle zusammengestellt. Tabelle 9 ist eine solche t-Tabelle.
Tabelle 9: Überschreitungswahrscheinlichkeiten für Abweichungen bestimmter Größe in t
|
t |
P(%) |
t |
P(%) |
|
0,1 |
92,0 |
2,1 |
3,6 |
|
0,2 |
84,1 |
2,2 |
2,8 |
|
0,3 |
76,3 |
2,3 |
2,1 |
|
0,4 |
68,8 |
2,4 |
1,6 |
|
0,5 |
61,8 |
2,5 |
1,2 |
|
0,6 |
55,0 |
2,6 |
0,93 |
|
0,7 |
48,3 |
2,7 |
0,70 |
|
0,8 |
42,4 |
2,8 |
0,52 |
|
0,9 |
36,8 |
2,9 |
0,38 |
|
1,0 |
31,7 |
3,0 |
0,27 |
|
1,1 |
27,1 |
3,1 |
0,19 |
|
1,2 |
23,0 |
3,2 |
0,14 |
|
1,3 |
19,3 |
3,3 |
0,10 |
|
1,4 |
16,0 |
3,4 |
0,067 |
|
1,5 |
13,2 |
3,5 |
0,049 |
|
1,6 |
11,0 |
3,6 |
0,032 |
|
1,7 |
8,9 |
3,7 |
0,021 |
|
1,8 |
7,2 |
3,8 |
0,014 |
|
1,9 |
5,7 |
3,9 |
0,0096 |
|
2,0 |
4,5 |
4,0 |
0,0064 |
Man bezeichnet derartige Verteilungen als Prüfverteilungen, t ist eine Prüfgröße. Die errechneten P-Werte gelten streng genommen nur für sehr große Stichproben, jedoch in guter Approximation auch für mittelgroße. Verwendet man den t-Wert daher in gewöhnlichen Stichproben, so führt das nur zu einem approximativen Test.
Zur Anwendung dieses Tests ist zunächst die Standardabweichung für die in Frage kommende Binomialverteilung zu errechnen, am besten anhand der Formeln (19) und (20). Bei dem vorher beschriebenen Beispiel ist n = 100, p = 0,8 und q = 0,2, demzufolge erhält man:
![]()
Danach errechnet man D, die Differenz zwischen Erwartung und Befund und dividiert diese durch die Standardabweichung. Der resultierende Quotient ist der t-Wert:
![]()
![]()
In Tabelle 9 findet man:
für t = 1,2 ein P von 23,0%
für t = 1,3 ein P von 19,3%
Durch lineare Interpolation ergibt sich für t = 1,25 ein P von 21,15 oder 0,2115.
Der exakte Test würde hier zu P = 0,2545 führen.
Die Entscheidung, wann eine Überschreitungswahrscheinlichkeit so klein ist, dass man die Hypothese ablehnen darf, kann letztlich nur der Experimentator selbst treffen. Es gibt jedoch eine (stillschweigende) internationale Übereinkunft über solche Grenzwerte. Man sagt, dass eine Differenz statistisch gesichert oder signifikant ist, falls die errechneten P-Werte zu klein sind, und bezeichnet:
| P < 0,05 | (= 5%) | als signifikant |
| P < 0,01 | (= 1%) | als gut (hoch) signifikant |
| P < 0,001 | (= 0,1%) | als sehr hoch signifikant |
Den soeben beschriebenen approximativen Test könnte man als „altdeutsches t-Verfahren“ bezeichnen. Er ist veraltet und wird nicht mehr so oft verwendet. Ein modernes Verfahren für die Lösung derartiger Testprobleme ist der . Er hat die gleiche logische Basis wie der t-Test ist aber erweiterungsfähiger. Wegen seiner großen Bedeutung wird das ausführlicher behandelt.
Das Kapitel „Grundbegriffe der Wahrscheinlichkeitsrechnung“ in pdf-Format. Grundbeg_Wahrscheinlichkeit.PDF