Das χ²-Verfahren zur Prüfung von Differenzen zu Erwartungswerten (Anpassungstest)
Das χ²-Verfahren ist ein universelles Verfahren zu biometrischen Prüfung von Häufigkeiten, wie sie sich bei der Auszählung der Stufen eines Merkmals mit diskreter Variation ergeben. Man berechnet die Prüfgröße χ² nach folgender Formel:
(21)
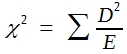
Bei dem Beispiel zum Unterschied des Impferfolges wurde ein Erfahrungswert mit dem bestehenden Impfverfahren von 80% erfolgreich immunisierter Tiere zugrunde gelegt, die neue Methode ergab einen Immunisierungserfolg von 85% Tieren. In diesem Beispiel sind für das χ²-Verfahren zur Sicherung von Unterschieden der Häufigkeiten folgende Rechenoperationen auszuführen: (G = gefundene Häufigkeit, E = Erwartungswert):
-
erfolgreich n. erfolgreich
Summe
G
85
15
100
E
80
20
100
D
+5
-5 0 D2
25 25 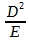
0,31 1,25
![]()
Dieser Wert ist das Quadrat des im Abschnitt oder berechnete t-Werte in Binomialverteilungen errechneten t-Wertes, was, bei Alternativmerkmalen stets der Fall ist.
Man vergleicht dann den gefundenen χ²-Wert mit den in der sogenannten χ²-Tabelle ablesbaren Grenzwerten für bestimmte Irrtumswahrscheinlichkeiten.
χ²-Tabelle: Werte von χ² für bestimmte Überschreitungswahrscheinlichkeiten
| Anzahl der
FG |
P=99% | P=5% | P=1% | P=0,1% |
|---|---|---|---|---|
| 1 | 0,00 | 3,84 | 6,64 | 10,83 |
| 2 | 0,02 | 5,99 | 9,21 | 13,82 |
| 3 | 0,12 | 7,82 | 11,34 | 16,27 |
| 4 | 0,30 | 9,49 | 13,28 | 18,47 |
| 5 | 0,55 | 11,07 | 15,09 | 20,52 |
| 6 | 0,87 | 12,59 | 16,81 | 22,46 |
| 7 | 1,24 | 14,07 | 18,48 | 24,32 |
| 8 | 1,65 | 15,51 | 20,09 | 26,12 |
| 9 | 2,09 | 16,92 | 21,67 | 27,88 |
| 10 | 2,56 | 18,31 | 23,21 | 29,59 |
| 11 | 3,05 | 19,68 | 24,72 | 31,26 |
| 12 | 3,57 | 21,03 | 26,22 | 32,91 |
| 13 | 4,11 | 22,36 | 27,69 | 34,53 |
| 14 | 4,66 | 23,68 | 29,14 | 36,12 |
| 15 | 5,23 | 25,00 | 30,58 | 37,70 |
| 16 | 5,81 | 26,30 | 32,00 | 39,25 |
| 17 | 6,41 | 27,59 | 33,41 | 40,79 |
| 18 | 7,02 | 28,87 | 34,80 | 42,31 |
| 19 | 7,63 | 30,14 | 36,19 | 43,82 |
| 20 | 8,26 | 31,41 | 37,57 | 45,32 |
| 21 | 8,90 | 32,67 | 38,93 | 46,80 |
| 22 | 9,54 | 33,92 | 40,29 | 48,27 |
| 23 | 10,20 | 35,17 | 41,64 | 49,73 |
| 24 | 10,86 | 36,42 | 42,98 | 51,18 |
| 25 | 11,52 | 37,65 | 44,31 | 52,62 |
| 26 | 12,20 | 38,88 | 45,64 | 54,05 |
| 27 | 12,88 | 40,11 | 46,96 | 55,48 |
| 28 | 13,56 | 41,34 | 48,28 | 56,89 |
| 29 | 14,26 | 42,56 | 49,59 | 58,30 |
| 30 | 14,95 | 43,77 | 50,89 | 59,70 |
Mit FG wird die Anzahl der Freiheitsgrade beschrieben. Eine Häufigkeitsverteilung mit 2 Alternativen besitzt einen Freiheitsgrad, da – wenn die Häufigkeit einer der beiden Alternativen gegeben ist – die Häufigkeit der anderen Alternative automatisch festliegt.
Für Alternativmerkmale gilt also die oberste Zeile der Tabelle. Wie ersichtlich ist unser χ²-Wert kleiner als 3,84, der Grenzwert für P=0,05. Demnach ist die Überschreitungswahrscheinlichkeit größer als 0,05 also 5% und die Differenz damit nicht signifikant.
Der Vorteil des -Testes besteht zunächst darin, dass man es auch für Merkmale mit mehr als 2 Variationsstufen verwenden kann. An die Stelle der Binomialverteilung tritt dann eine Multinomialverteilung. Als Beispiel soll die Berechnung von bei einer Verteilung von 3 Merkmalsklassen dienen, wie sie sich bei der Prüfung einer genetischen Aufspaltung mit intermediärem Erbgang ergibt. Nach der genetischen Theorie erwartet man bekanntlich eine 1:2:1 Spaltung, bzw. p=0,25; q=0,5 und r=0,25.
Bitte nehmen Sie nun an, dass in einem speziellen Fall 32 AA, 94 Aa und 34 aa-Pflanzen gefunden wurden. Es müssen dann zuerst die Erwartungswerte berechnet werden. Man erhält:
n = 32 + 94 + 34 = 160
und demnach
![]()
![]()
![]()
Danach findet man:
|
|
AA |
Aa |
aa |
Summe |
|---|---|---|---|---|
| G | 32 | 94 | 34 | 160 |
| E | 40 | 80 | 40 | 160 |
| D | -8 | +14 | -6 | 0 |
| D2 | 64 | 196 | 36 | |
|
1,60 |
2,45 |
0,90 |
|
![]()
Hier setzt sich χ² aus 3 Summanden zusammen. Demzufolge ergeben sich auch rein zufällig größere Werte und man benötigt andere Grenzwerte als bei einer Binomialverteilung. Man findet diese in der zweiten Zeile der Tabelle und stellt fest, dass der Grenzwert für P=0,05 jetzt 5,99 ist. Somit sind auch bei diesem Beispiel die Abweichungen von der erwarteten 1:2:1-Spaltung nicht signifikant.
Beim χ²-Verfahren benützt man die Bezeichnung Freiheitsgrade (=FG). Die FG sind bei den hier besprochenen Beispielen die um 1 verminderte Zahl der Merkmalsklassen. Übrigens bezeichnet man diese Anwendungsform des χ²-Tests , bei der die Unterschiede zwischen den gefundenen Häufigkeiten und den aufgrund einer biologisch sinnvollen Hypothese zu erwartenden als Anpassungstest.
Homogenitätstest
In der Praxis wissenschaftlicher Forschungstätigkeit gibt es oft keine eindeutige Hypothese über die Wahrscheinlichkeiten und folglich auch keinen Ansatzpunkt für die Errechnung von Erwartungswerten. Dann muss man die Untersuchung so durchführen, dass man mehrere Stichproben erhält. Es gilt dann zu prüfen, ob die gefundenen Häufigkeiten von Stichprobe zu Stichprobe differieren. Die Null-Hypothese würde in diesem Fall lauten: Alle Stichproben entstammen der gleichen Grundgesamtheit, die gefundenen Unterschiede in den relativen Häufigkeiten sind zufällig. Derartige Hypothesen prüft man mittels einer anderen Anwendungsform des χ²-Tests, die als Homogenitätstest bezeichnet wird.
Als Beispiel sei angenommen, dass zu prüfen war, ob zwei Bullen sich in ihrer Fertilität unterscheiden. Zur Überprüfung dieser Frage eignet sich das Erstbesamungsergebnis (EBE), die Zahl der besamten Kühe, die sofort trächtig wurden. Die Prüfung brachte folgendes Ergebnis:
Bulle 1: positiv 97, negativ 23 EBE = 81%
Bulle 2: positiv 53, negativ 27 EBE = 66%
Die Frage lautet, ob es unwahrscheinlich ist, dass so große Differenzen rein zufällig auftreten. Die mutmaßlichen Wahrscheinlichkeitswerte einer Grundgesamtheit, aus der beide Stichproben stammen, ergeben sich aus der Addition der gefundenen Häufigkeiten. Man erhält:
![]()
![]()
![]()
Und daher:
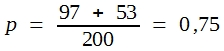
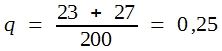
Wenn man diese Wahrscheinlichkeitswerte mit n1 und n2 multipliziert, bekommt man die 4 Erwartungswerte.
In der Praxis bildet man die sogenannten Randsummen und errechnet dann die Erwartungswerte für die Zellen nach der Dreisatzrechnung. Hier erhält man:
|
97 |
23 | 120 |
| 53 | 27 | 80 |
| 150 | 50 | 200 |
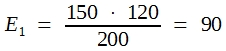
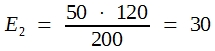
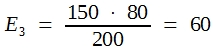
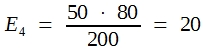
Man rechnet wie folgt weiter:
|
G |
E |
D |
D2 |
||||||
|
97 |
23 |
90 |
30 |
+7 |
-7 |
49 |
49 |
0,54 |
1,63 |
|
53 |
27 |
60 |
20 |
-7 |
+7 |
49 |
49 |
0,82 |
2,45 |
| χ² = 5,44 | |||||||||
Von den 4 Häufigkeiten sind 3 durch die Randsummen festgelegt. Demnach haben wir nur einen frei variablen Wert, nur 1 FG. Das aber bedeutet, dass das errechnete χ² von 5,44 größer als der Tabellenwert 3,84 für P=5% ist. Die Differenzen zwischen den beiden Stichproben sind daher signifikant, die Null-Hypothese, nach der beide der gleichen Grundgesamtheit entstammen, ist abzulehnen.
Falls Ihnen die Berechnung der Freiheitsgrade beim Homogenitätstest Schwierigkeiten bereitet, sei folgendes Verfahren empfohlen: Schreiben Sie bitte die Häufigkeitszahlen in ein zweidimensionales Schema und streichen Sie dann von rechts eine Spalte und von unten eine Zeile ab. Die Anzahl der danach im linken oberen Quadranten stehenden Werte entspricht der Anzahl der Freiheitsgrade. In der folgenden Abbildung handelt es sich um 3 Stichproben mit je 4 Werten. Es gibt dann, wie man sieht, 6 Freiheitsgrade.
|
x |
x |
x |
x |
|
|---|---|---|---|---|
|
x |
x |
x |
x |
|
|
x |
x |
x |
x |
|
Bemerkungen zum Einsatz des χ²-Verfahrens
Das χ²-Verfahren stellt eine vielseitig verwendbare Methode zur biometrischen Prüfung von Häufigkeiten dar, es sei aber auch betont, dass es sich hier lediglich um einen approximativen Test handelt. Schon deshalb ist es notwendig, die Frage zu erörtern, wann die so errechneten Näherungswerte für die Überschreitungswahrscheinlichkeiten gut sind.
Zunächst darf man sagen, dass die Differenzen zwischen dem Ergebnis eines exakten Tests und dem der approximativen χ²-Tests mit wachsendem Stichprobenumfang immer geringer werden. Die Werte sind exakt, wenn n unendlich groß ist. Bei gegebenem Stichprobenumfang ist die Näherung dann am besten, wenn p = q = 0,5 ist, sie wird schlechter, wenn p von q sehr verschieden ist. In Kombination beider Kriterien gilt als Faustzahl für die Grenze des Einsatzes des χ²-Verfahrens:
A: Verwende χ² bei einer Binomialverteilung nur dann, wenn np und nq > 10 sind.
Das bedeutet, dass man bei p = q = 0,5 bereits von n = 21 ab, bei p = 0,75 und daher q = 0,25 dagegen erst von n = 41 ab verwenden darf.
Für Verteilungen mit mehr als 2 Klassen ist die unter A definierte Forderung zu scharf.
Hier genügt es, wenn alle Erwartungswerte größer als 5 sind. Eine zweite Faustzahl lässt sich daher wie folgt formulieren:
B: Verwende χ² bei Multinomialverteilungen nur dann, wenn alle Erwartungswerte > 5 sind.
Bitte beachten Sie jedoch, dass sich diese Regeln auf die Erwartungswerte beziehen, nicht auf die gefundenen Häufigkeiten.
Sind damit die Grenzen der Anwendbarkeit des χ²-Verfahrens abgesteckt, so erhebt sich die Frage, was zu tun ist, wenn in einem speziellen Fall die genannten Bedingungen nicht erfüllt sind. Es gibt darauf zwei verschiedene Antworten. Zunächst ist es stets möglich, die Überschreitungswahrscheinlichkeiten exakt zu errechnen. Das Verfahren wurde hier lediglich für Binomialverteilungen besprochen (siehe). Es lässt sich aber auf Multinomialverteilungen erweitern. Allerdings ist der Rechenaufwand dann noch höher, sodass es zweckmäßig ist, EDV-Anlagen einzusetzen.
Eine andere Antwort auf die Frage, was zu tun ist, wenn die Bedingungen zum Einsatz des χ²-Verfahrens nicht erfüllt sind, beschränkt sich auf solche Verteilungen, bei denen χ² nur 1 FG hat. Man kann dann nach einem Vorschlag von YATES ein korrigiertes χ² berechnen, das auch bei kleinen Stichproben gut Testergebnisse liefert. Man rechnet nach folgender Formel:
(22)
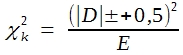
Vom Betrag der Differenz ist also vor dem Quadrieren 0,5 zu subtrahieren. Die so ermittelten Testergebnisse sind nicht generell präziser als die nach dem gewöhnlichen χ²-Verfahren auszurechnenden. Lediglich im Bereich zwischen 1 und 10% Überschreitungswahrscheinlichkeit stimmen die Resultate besser mit denen eines exakten Tests überein, gerade auf diesen Bereich kommt es aber in der Regel an.
Vor der Anwendung des χ²-Verfahrens ist stets zu prüfen, ob die zu testenden Häufigkeitsdifferenzen voneinander stochastisch unabhängig sind. Die Gefahr, dass das nicht der Fall ist, besteht bei Tierversuchen z.B. dann, wenn die Beobachtungen an mehreren Tieren, aber auch mehrfach an jedem Einzeltier durchgeführt werden. Man muss immer damit rechnen, dass die Wahrscheinlichkeiten für das Eintreffen der Ereignisse von Tier zu Tier unterschiedlich sind. Dadurch ändern sich die Überschreitungswahrscheinlichkeiten für Abweichungen bestimmten Ausmaßes und die Grenzwerte der χ²-Tabelle können falsch werden.
Nach der Anwendung des ist sorgfältig zu überdenken, welche Schlussfolgerungen aus den Testergebnissen gezogen werden dürfen. Nicht selten bestehen etwas unterschiedliche Grundbedingungen bei den in Vergleich gebrachten Stichproben. Man vergleicht dann Häufigkeiten, die eigentlich nicht vergleichbar sind, und darf auch aus hoch signifikanten Differenzen nicht ohne weiteres die im Sinne der Untersuchung liegenden Schlussfolgerungen ziehen.
Merksatz: Das Aufsuchen von signifikanten Differenzen aus Stichproben, die nicht ganz miteinander vergleichbar sind, und die leichtfertige Interpretation ihrer möglichen Ursachen führt oft zu statistischen Fälschungen.
Abschätzung des optimalen Stichprobenumfangs
Wenn in einem Vorversuch auf die Behandlung A 3 von 7 Tiere reagiert haben und unter der Behandlung B 4 von 7 Tieren reagieren kann wird man mithilfe des χ²-Verfahrens die Erfolgsquoten einander gegenüberstellen.
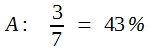
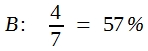
Es kann in Zweifel gezogen werden, ob man aufgrund dieser Differenz behaupten darf, dass Methode B besser sei als Methode A. Mithilfe des χ²-Verfahrens kann man diese Frage zunächst überprüfen, indem man einen Homogenitätstest durchführt. Die Rechnung ergibt:
|
3 |
4 |
7 |
|---|---|---|
|
4 |
3 |
7 |
|
7 |
7 |
14 |
![]()
|
G |
E |
D |
D2 |
||||||
|
3 |
4 |
3,5 |
3,5 |
-0,5 |
+0,5 |
0,25 |
0,25 |
0,0714 |
0,0714 |
|
4 |
3 |
3,5 |
3,5 |
+0,5 |
-0,5 |
0,25 |
0,25 |
0,0714 |
0,0714 |
![]()
Dieser Wert ist natürlich nicht signifikant, sodass man vorläufig annehmen muss, dass Unterschiede in den gefundenen Häufigkeiten nur zufällig sind.
Es ist damit jedoch nicht bewiesen, dass es keine echten Häufigkeitsdifferenzen gibt. Es könnte also sein, dass der Versuchsansteller nach wie vor überzeugt ist, dass die Differenzen in der gefundenen Größe vorliegen und dafür seinen Grund hat. Er wird dann ein weiteres, größeres Experiment durchführen wollen, und möchte wissen, wie groß die Stichproben sein müssen, damit Differenzen in der errechneten Größe, d.h. 43:57%, signifikant werden.
Zwischen χ² und der Stichprobengröße besteht eine lineare Proportionalität. Eine Verdopplung der Versuchstierzahl führt prozentual zu dem gleichen Versuchsergebnis auch zu einer Verdopplung des χ²-Wertes . Laut χ²-Tabelle beträgt bei 1 FG der Grenzwert für 5% Irrtumswahrscheinlichkeit 3,84. Bezeichnet man das im Vorversuch gefundene χ² als χ²1 , den Grenzwert in der Tabelle als χ²G, dann verhält sich
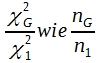
wobei n1 die Stichprobengröße des Vorversuchs ist, nG der zur Erzielung einer signifikanten Differenz erforderliche Stichprobenumfang. Man erhält folglich:
(23)
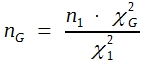
Im Beispiel ergibt sich daraus:
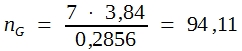
Somit sind etwa 95 Tiere für jede der beiden Behandlungsgruppen erforderlich, um Häufigkeitsunterschiede, wie sie im Vorversuch gefunden wurden, als signifikant nachweisen zu können.
Damit soll jedoch nicht behauptet werden, dass die im Vorversuch gefundenen Differenzen echt sein müssen und man das zweite Experiment lediglich durchführt, um etwas beweisen zu können, was dem Versuchsansteller längst bekannt ist. Es gibt aber Fälle, wo dieser konkrete Vermutungen über Richtung und Ausmaß bestimmter Häufigkeitsdifferenzen hat. Formel (23) gibt ihm dann die Möglichkeit, den notwendigen Umfang des zur Prüfung seiner Vermutung durchzuführenden Experiments abzuschätzen. Der Versuchsansteller kann damit seine Arbeit rationalisieren. Da wissenschaftliche Untersuchungen immer teurer werden, bekommen solche biometrischen Berechnungen zur Planung experimenteller Untersuchungen eine schnell wachsende Bedeutung.
Weiter Anmerkungen zur Verwendung der Tests:
Außer den aufgeführten Hinweisen zum erforderlichen Mindestumfang der Stichproben und Einzelhäufigkeiten gelten die folgende Zusammenfassung:
- Für alle Chi²-Tests gilt: Die zu untersuchende Stichprobe muss in Häufigkeiten vorliegen. Häufigkeiten werden in ganzen, natürlichen Zahlen ausgedrückt.
- Gibt es eine Erwartung an die Verteilung der Häufigkeiten in der Stichprobe wird der Chi²-Anpassungstest gerechnet. Eine Erwartung kann vorliegen, wenn zum Beispiel biologische, chemische und physikalische dies Vorgeben oder zum Beispiel umfangreiche Erfahrungen dies nahelegt.
- Als Grundannahme (Nullhypothese) gilt: Die in der Stichprobe beobachtete Verteilung der Häufigkeiten stimmt mit der Grundannahme überein. Beobachtete Abweichungen sind zufällig.
- Wenn es KEINE Erwartung an die Verteilung der Häufigkeiten gibt, müssen wenigstens 2 Stichproben vorliegen, die auf Übereinstimmung geprüft werden können.
- Als Grundannahme (Nullhypothese) gilt: Die Stichproben unterscheiden sich nicht signifikant voneinander. Beobachtete Abweichungen sind zufällig entstanden. Nur unter dieser Voraussetzung können aus der Zusammenfassung der zu vergleichenden Stichproben neue Erwartungswerte berechnet werden.
- Zeigt sich durch den Test, dass die beobachten Unterschiede der beobachteten Häufigkeitsverteilungen zu den erwarteten Häufigkeitsverteilungen mit einer Wahrscheinlichkeit von weniger als 5% durch Zufall bedingt sind, verwerfen wir die Nullhypothese und sprechen von einem signifikanten Unterschied. Unterschiede in der gefundenen Art kommen rein zufällig in weniger als 5% der Fälle vor. Es besteht somit aber immer das Risiko, dass wir uns mit dieser Behauptung irren, aber das kommt nur jedes 20-te Mal vor. Weitere übliche Grenzen der Überschreitungswahrscheinlichkeit liegen bei 1% (hoch/gut signifikant) und 0,1% (sehr hoch/gut signifikant).
PDF-Version zum Herunterladen: Pruefung_von_Haeufigkeiten