Gleich oder nicht gleich, das ist hier die Frage?
Vergleich von Stichprobenmittelwerten mithilfe des t-Tests
Für den Vergleich von Mittelwerten setzen Sie den student’schen t-Test dann ein, wenn
- Sie die aus mehreren Messwerten erhalten wurden,
- angenommen werden kann, dass alle Messwerte der gleichen Grundgesamtheit entstammen.
- vorausgesetzt werden kann, dass die Messwerte (die Grundesamtheit) hinreichend normalverteilt sind.
In diesem Versuch geht es um die Entscheidung, ob die Massegehalte zweier Lösungen gleich sind. Vergleiche dieser Art verwenden Sie bei Tests auf die Wirksamkeit von Wachstumsfaktoren im Hafer-Coleoptilentest, bei der Suche nach geeigneten Ersatzstoffen, zum Vergleich in Testsystemen (Referenzmaterialien, Kalibratoren etc.), die biologisch, immunologisch oder chemisch, in jedem Fall aber quantitativ aufgebaut sind.
Für den heutigen Versuchstag stehen 3 Testlösungen aus, von denen Sie genau zwei untersuchen sollen. Es handelt sich um verdünnte Salzsäurelösungen, wie sie zum Beispiel bei der Bestimmung der titrierbaren Säure in Sauerkraut oder Tomatenmark zu untersuchen wären. Der Säurekonzentration beträgt ungefähr 0,1 Mol / Liter, was einem pH von 1 entspricht. In Lebensmitteln findet sich ein Gemisch meist organischer Säuren wie Essigsäure, Milchsäure, Weinsäure etc., die meist summarisch erfasst werden.
Gegeben sind als „Ersatz“ für die Säuregemische natürlichen Urprungs die Lösungen „A“; „B“ und „C“.
Ihre Aufgabe besteht in der Überprüfung der Konzentrationsgleichheit zweier gegebener Lösungen.
Bei dieser Übung kommt es nicht auf die exakte Bestimmung einer Konzentration an, deshalb reicht es aus, eine Natronlauge mit ungefähr 0,1 mol / Liter als Titrationsmittel anzusetzen. Sollte diese Natronlauge nicht ausstehen, setzen Sie diese selbst an. Geben Sie als Einwaage von 4 g NaOH (beachten Sie die fehlenden Nachkommastellen!) in ein Plastikgefäß und lösen in circa 0,5 Liter demineralisiertem Wasser. Geben Sie diese Lösung in einen geeigneten Messkolben (1 Liter) und füllen diesen bis zur Marke mit demineralisiertem Wasser auf. Die erreichte Genauigkeit ist für diesen Versuch vollkommen ausreichend. Ein Faktor braucht nicht bestimmt zu werden! Die Natronlauge sollte keinesfalls in einem Glasgefäß gelagert werden. Zu diesem Zweck sind Gefäße auf Polypropylen und Polyethylen besser geeignet. Welche Auswirkungen hätte ein neuerliches Ansetzen des Titrationsmittels für die Aussage des Tests?
Durchführung:
Pipettieren Sie jeweils 10,00 ml der für Sie benannten Lösung 1 in einen circa 250 ml Erlenmeyerkolben.
Geben Sie 1-3 Tropfen Indikatorlösung (Phenolphthalein) in den Erlenmeyerkolben und
fügen bei Bedarf etwas demineralisiertes Wasser hinzu.
Verfahren Sie mit der von Ihnen angesetzten Natronlauge entsprechend dem im Praktikum erlernten Verfahren zur Titration von Säuren.
Bestimmen Sie den Verbrauch an Natronlauge in jeweils 5 Titrationen mit den beiden Ihnen genannten zu untersuchenden Lösungen.
Geben Sie die Titrationsvolumina mit geschätzten 2 Nachkommastellen an.
Protokoll- und Lösungsblatt
Name: ………………………………. Datum: …………..
Klasse: ………………
Lösung 1 hat die Bezeichnung: ____
Lösung 2 hat die Bezeichnung: ____
Natronlaugeverbrauch für:
| Verbr. 1 | Verbr. 2 | Verbr. 3 | Verbr. 4 | Verbr. 5 |  |
Varianz | |
| Lösung 1 | |||||||
| Lösung 2 |
Der mittlere Verbrauch für die Titration von Lösung 1 betrug _______ ml bei einer Streuung (Standardabweichung) von _____ ml.
Der mittlere Verbrauch für die Titration von Lösung 2 betrug _______ ml bei einer Streuung (Standardabweichung) von _____ ml.
Der Median/Zentralwert der Titrationen von Lösung 1 betrug _____ ml.
Die Variationsbreite der Titrationen von Lösung 1 betrug _____ ml.
Der Median/Zentralwert der Titrationen von Lösung 2 betrug _____ ml.
Die Variationsbreite der Titrationen von Lösung 2 betrug _____ ml.
Sie können die Standardabweichung nach der Formel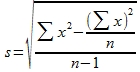 
berechnen.
Die Differenz der Mittelwerte beträgt: _____ ml.
Die Standardabweichung der Differenz berechnen Sie mit: 
zu _____ ml.
Der t-Wert ergibt sich aus: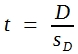 
zu _____.
Die Anzahl der Freiheitsgrade beträgt 
also _____ .
Der Vergleichswert aus der t-Tabelle für FG-Freiheitsgrade und die damit von Ihnen gewählte Signifikanzgrenze beträgt _____ .
Welche Schlussfolgerung ergibt sich für die von Ihnen untersuchten Lösungen?
_______________________________________________________________________
_______________________________________________________________________
PDF-Version: t_TestPraktikum